Обратная матрица

Определение 14.8 Матрица 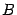называется обратной матрицей для квадратной матрицы 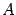, если .

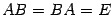Из определения следует, что обратная матрица 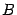будет квадратной матрицей того же порядка, что и матрица 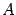(иначе одно из произведени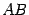й или 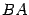было бы не определено).

Обратная матрица для матрицы 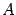обозначается 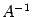. Таким образом, если 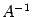существует, то .

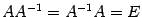Из определения обратной матрицы следует, что матрица 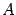является обратной для матрицы 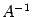, то есть 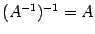. Про матрицы 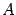и 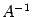можно говорить, что они обратны друг другу или взаимно обратны.

Предложение 14.20 Если матрица 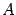имеет обратную, то 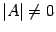и .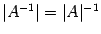

Доказательство. Так как определитель произведения матриц равен произведению определителей (предложение 14.7), то 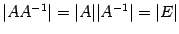. По следствию 14.1 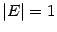, поэтому 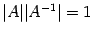, что невозможно при 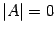. Из предыдущего равенства следует также .

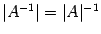Последнее предложение можно сформулировать в следующем виде.