Функции одной переменной. Необходимые и достаточные условия

Функция f (x) имеет локальный минимум в точке x₀, если существует некоторая положительная величина , такая, что если |x - x₀| < , то f (x)>= f (x₀), если существует окрестность точки x₀, такая, что для всех значений x в этой окрестности f(x) > f(x₀). Функция f(x) имеет глобальный минимум в точке x*, если для всех x справедливо неравенство f(x)>=f(x*).

На рис.2.8 дано графическое представление функции f(x), которая имеет локальный минимум в точке x₀ и глобальный минимум в точке x*.

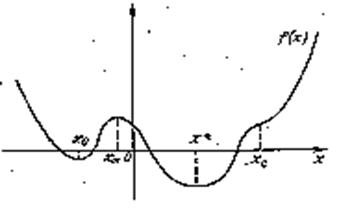
Рисунок 2.8 - Графическое представление функции

Классический подход к задаче нахождения значений x₀ и x* состоит в поиске уравнений, которым они должны удовлетворять. Представленная на рис.2.8 функция и ее производные непрерывны, и видно, что в точках x₀ и x* будут решениями уравнения

f' (x)=0 (2.1)

Точка x_m, в которой достигается локальный минимум, и точка x_c, в которой имеется точка горизонтального перегиба функции, также удовлетворяет этому уравнению. Следовательно, уравнение (2.1) является только необходимым условием, но не является достаточным условием.

Заметим, однако, что в точках x₀ и x* производная f' (x) меняет знак с отрицательного на положительный. В точке x_m знак меняется с положительного на отрицательный, в то время как в точке x_c он не меняется. Следовательно, производная в минимуме является возрастающей функцией, а поскольку степень возрастания f' (x) измеряется второй производной, можно ожидать, что f'' (x₀)>0,
f'' (x*)>0, тогда как f'' (x) <0.

Если, однако, вторая производная равна нулю, ситуация остается неопределенной.

Полученные выше результаты могут найти надежное обоснование, если рассмотреть разложение функции f (x) в ряд Тейлора в окрестности точки x₀ (или x*, или x_m), что, конечно, требует непрерывности функции f (x) и ее производных:

f (x₀ + h) - f (x₀) = h f' (x)+(h²/2!) f'' (x₀)+... (2.2)

Если в точке x₀ достигается минимум, то левая часть (2.2) будет неотрицательной для любого достаточно малого h (|h|<). Следовательно, первая производная f' (x₀) должна быть равна нулю, и это и есть достаточное условие (см. уравнение 2.1). Если бы она была положительной, то достаточно малое отрицательное значение h делало бы правую часть (2.2) отрицательной, а если бы она была отрицательной, то достаточно малое положительное значение h делало бы ее отрицательной.

Так как в следующем члене (2.2) всегда h₂ > 0, то, если

f'' (x*)>0, (2.3)

в точке x0 достигается минимум. Если f' (x_m) = 0 и f'' (x_m) < 0, то из аналогичных соображений в точке x_m достигается максимум. Для определения различия между локальным и глобальным минимумами необходимо сравнить значения функций f (x₀) и f (x*).