Решение. Вероятность появления «герба» при одном бросании монеты равна 0,5

Вероятность появления «герба» при одном бросании монеты равна 0,5. В серии из 4 подбрасываний монеты случайная величина Х может принимать следующие значения: 0,1,2,3,4. Чтобы составить закон распределения с.в. Х, нужно найти вероятности этих событий:

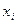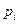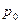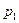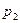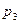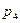Воспользуемся формулой Бернулли для вычисления всех вероятностей:

Итак, теперь мы можем записать закон распределения случайной величины Х:

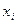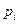	0,0625	0,25	0,375	0,25	0,0625

Сделаем проверку:

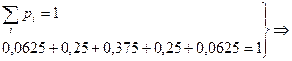- условие нормировки выполнено.

Найдем функцию распределения с.в. Х. По определению функции распределения:

Рассмотрим несколько промежутков значений для х:

· при

· при

· при

· при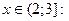

· при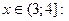

· при

Итак, запишем функцию распределения:

Построим ее график:

Вычислим математическое ожидание случайной величины Х:

Используя свойство дисперсии, вычислим ее:

Задача 12.2.2. Закон распределения случайной величины Х имеет вид:

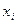	-2	-1
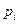	0,2	0,1	0,2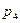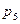

Найти вероятности 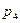, 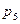и дисперсию D(X), если математическое ожидание М(Х)=2,1.