а) Неизвестный параметр найдем из условия нормировки:
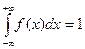
В нашем случае:
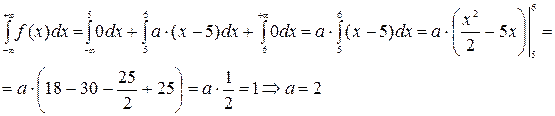
Запишем вид функции плотности распределения с уже найденным параметром а:
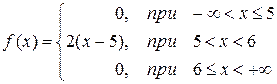
б) Функция распределения связана с функцией плотности следующим соотношением:
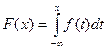
Тогда в нашем случае:
· при 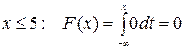
· при 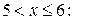
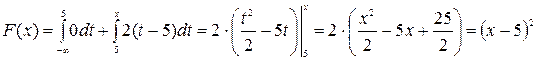
· при 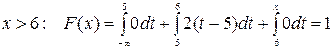
Итак, функция распределения имеет следующий вид:
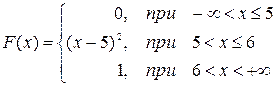
в) Вероятность попадания случайной величины в интервал вычисляется по формуле:
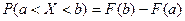
В нашем случае:
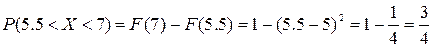
г) Математическое ожидание непрерывной случайной величины Х вычисляется по формуле:
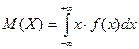
В нашем случае:
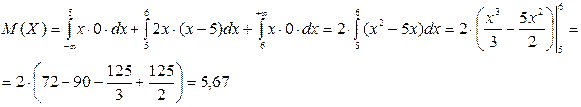
По свойству дисперсии:
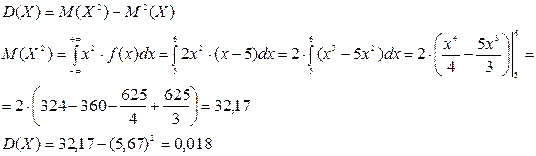
Построим графики функций f(x) и F(x).

 Задача 12.2.4. Случайные величины
Задача 12.2.4. Случайные величины 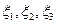 имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания M(ξi)=6, а дисперсия D(ξ1)=1/3. Найти вероятности: а)
имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания M(ξi)=6, а дисперсия D(ξ1)=1/3. Найти вероятности: а) 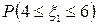 ; б)
; б) 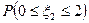 ; в)
; в) 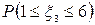 .
.
 2015-01-30
2015-01-30 5619
5619








