2015-01-30
1915
Неизвестные вероятности будем искать, исходя из условия нормировки и определения математического ожидания:
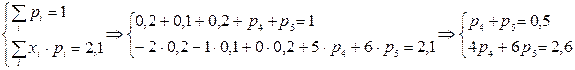
Решая систему, находим вероятности:
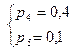
Значит, закон распределения с.в. Х имеет вид:
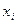 | -2 | -1 | |||
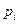 | 0,2 | 0,1 | 0,2 | 0,4 | 0,1 |
Найдем дисперсию D(X):
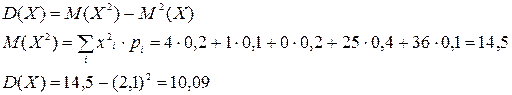
Ответ: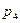 
=0,4,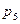 
=0,1, D(X)=10,09
Задача 12.2.3. Плотность распределения непрерывной случайной величины Х имеет вид:
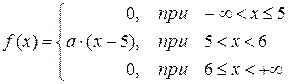
Найти:
а) параметр а,
б) функцию распределения F(x),
в) вероятность попадания случайной величины Х в интервал (5,5; 7),
г) математическое ожидание М(Х) и дисперсию D(X).
Построить графики функций f(x) и F(x).
