Решение систем линейных алгебраических уравнений

Рассмотрим систему уравнений: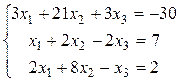

В программе такую систему надо набрать в текстовом редакторе.

Пример 7. Решение системы линейных алгебраических уравнений матричным методом.

Заданная система уравнений может быть представлена в матричной форме:

А×х=В,

Где

А= 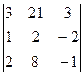- матрица коэффициентов системы;

х= 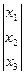- вектор-столбец вычисляемого решения системы (не вводится);

В= 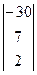- вектор-столбец свободных членов системы.

Решение системы получим в виде матричного уравнения: х=А^-1×В

Порядок выполнения:

Вызвать математическую панель инструментов Мatrix(Матрицы).

Ввести элементы матриц А и В, используя опыт, приобретенный при решении задач 4.1, 4.2.

А:= 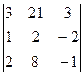В:=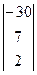

Набрать с клавиатуры матричное уравнение:

х:=А^-1×В

Ввести с клавиатуры:

х=

На экране появится вектор корней системы уравнений х₁, х₂, х₃:

х=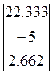

Заметим, как говорилось ранее, в векторе х стоят элементы со смещенными индексами: х₀, х₁, х₂. Таким образом, в соответствии с исходными обозначениями мы получили решение заданной системы линейных алгебраических уравнений:

х₁=22,333; х₂=-5; х₃=2,662

Проверка: Набрать с клавиатуры А×х=, получим:

× Аּх=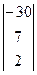

Результат совпал с исходным вектором свободных членов В. Следовательно, система решена правильно.