Геометрические вероятности. Очень часто при определении пространства элементарных исходов оказывается невозможным перенумеровать все результаты проводимого эксперимента

Очень часто при определении пространства элементарных исходов оказывается невозможным перенумеровать все результаты проводимого эксперимента, однако удается задать это множество в виде некоторого геометрического объекта (отрезка, многоугольника, многогранника). Для определенности давайте считать, что Ω – некоторый многоугольник. В этом случае вероятность события А определяется так:

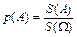. Если же площадь множества А невозможно измерить (а в математике случается и такое), то множество А не считается событием. То есть в данном случае событием является не любое подмножество пространства элементарных исходов, а только то подмножество, площадь которого можно измерить.

Приложение 2.

Контрольная работа по теории вероятностей (проводилась в 2001 году в 11б классе сш №17 г. Твери).

Вариант 1

1. Р(А)=0,6; Р(В)=0,4; Р(АВ)=0,2. Найти Р(А+В), .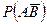

2. Вероятностное пространство состоит из 4 элементарных исходов: 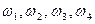, вероятности которых пропорциональны числам 1, 2, 3 и 4. 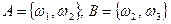. Найти Р(А½В). Будут ли события А и В независимы?

3. В 11б классе случайным образом выбирают одного мальчика и одну девочку для участия в игре «Счастливый случай». Какова вероятность, что это будут Саша и Настя? Какова вероятность, что среди них будет Лена или Олег? (В 11б классе 8 девочек и 17 мальчиков, из них 3 Насти, 2 Лены, 3 Саши и 3 Олега).

4. В коробке 10 красных и 6 синих шаров. Ваня достает 5 шаров. Какова вероятность, что он вытащит ровно 2 синих шара? Какова вероятность, что он вытащит хотя бы один синий шар?

5. Вероятность того, что богатая невеста имеет плохой характер, равна 0,8; бедная – 0,4. В Твери 20% богатых и 80% бедных невест. Ваня женился на первой встречной и, увы, ему досталась жена с плохим характером. Какова вероятность, что она богата?

6. Кубик кидают 4 раза. Какова вероятность, что ровно 2 раза выпадет шестерка?

Вариант 2

1. Р(А)=0,5; Р(В)=0,4; Р(А+В)=0,7. Найти Р(АВ), .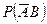

2. Вероятностное пространство состоит из 4 элементарных исходов: 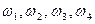, вероятности которых пропорциональны числам 1, 2, 2 и 3. 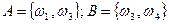. Найти Р(А½В). Будут ли события А и В независимы?

3. Василий Сергеевич случайным образом построил в шеренгу трех Антонов и трех Дим. Какова вероятность, Дима Сапожников и Антон Цуканов будут стоять рядом? Какова вероятность, что Антон Кошелев будет стоять с краю?

4. В коробке 2 красных и 3 синих шара. Двое ученых по очереди тащат шары, пока не вытащат красный. Какова вероятность, что первым это сделает первый ученый?

5. 2 раза в неделю Андрей Клишов готовит уроки. Если он идет в школу с выученными уроками, то вероятность получить пятерку равна 0,7; если с невыученными – то 0,2. Известно, что в субботу Андрей получил пятерку. Какова вероятность, что в этот день он выучил уроки?

6. Кубик кидают 10 раз. Какова вероятность, что шестерка выпадет хотя бы раз? Что она выпадет ровно 1 раз?

Вариант 3

1. Р(А)=0,6; Р(В)=0,4; А и В независимы. Найти Р(А+В), .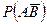

2. Вероятностное пространство состоит из 4 элементарных исходов: 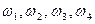. . 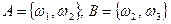Известно, что Р(w₁)=0,4, Р(w₃)=0,2, Р(А½В)=0,5. Найти Р(А) и Р(В).

3. В 11б классе случайным образом выбирают двух мальчиков и двух девочек для проверки уровня математической подготовки. Какова вероятность, что среди них будут Арина и Олег? (В 11б классе одна Арина; остальные сведения в задаче из 1 варианта).

4. В коробке 6 красных и 8 синих шаров. Ваня достает 3 шара. Какова вероятность, что он вытащит 3 шара одного цвета? Какова вероятность, что он вытащит ровно один синий шар?

5. Денис решает правильно одну задачу из трех, Гриша – одну из двух, а Андрей – одну из шести. Андрей списывает в среднем две задачи из пяти, причем одинаково часто у Гриши и у Дениса. На этот раз задача у Андрея оказалась решенной правильно. Какова вероятность, что он ее списал у Гриши?

6. Имеются 4 карточки с буквами М, А, Ш и А. Маша в произвольном порядке выкладывает их на стол. Какова вероятность, что получится слово МАША?

Вариант 4

1. Р(А)=0,6; Р(В)=0,4; Р(А½В)=0,5. Найти Р(А+В), .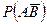

2. Вероятностное пространство состоит из 4 элементарных исходов: 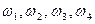. . 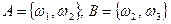Известно, что Р(w₁)= 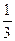, Р(w₃)= 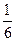, А и В независимы. Найти вероятности всех элементарных исходов.

3. В 11б классе случайным образом выбирают двух мальчиков и двух девочек для проверки уровня физической подготовки. Какова вероятность, что среди них будут две Насти и ни одного Димы? (В 11б классе 3 Димы).

4. В коробке 4 красных и 6 синих шаров. Ваня достает 4 шара. Какова вероятность, что среди них синих шаров окажется больше? Какова вероятность, что синих шаров не будет совсем?

5. У Саши Годикова в левом кармане 4 шпаргалки по физике и 6 по химии, а в правом 2 шпаргалки по химии и шесть по физике. Саша достает из левого кармана одну шпаргалку и, если она по физике, то кладет ее на место, а если по химии, то перекладывает в другой карман. После чего он достает шпаргалку из правого кармана. Известно, что это была шпаргалка по химии. Какова вероятность, что из левого кармана он тоже достал шпаргалку по химии?

6. Имеются 4 карточки с буквами А, Н, Т, О и Н. Антон в произвольном порядке выкладывает их на стол. Какова вероятность, что получится слово ТОННА?