И законы электродинамики

Механический принцип относительности

Во второй половине XIX века Д. Максвеллом были сформулированы основные законы электродинамики. При этом возникли сомнения в справедливости механического принципа относительности Галилея применительно к электромагнитным явлениям. Вспомним суть механического принципа относительности.

Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны); в этом состоит суть механического принципа относительности или принципа относительности Галилея.

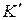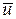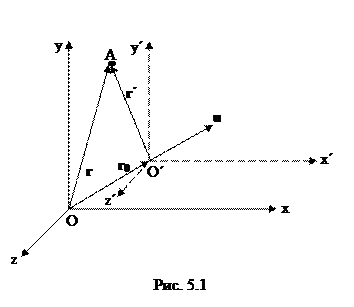
Для доказательства этого принципа рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), которую условно будем считать неподвижной и подвижную систему (с координатами ), движущуюся относительно К равномерно и прямолинейно со скоростью = const. Примем, что в начальный момент времени t = 0 начала О и 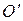обеих систем координат совпадают. Расположение систем координат в произвольный момент времени t имеет вид, изображенный на рис. 5.1. Скорость 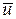направлена вдоль прямой 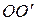, а радиус-вектор, проведенный из точки О в точку 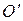, равен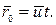

Координаты произвольной материальной точки А в неподвижной и подвижной системах отсчета определяются радиусами-векторам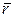и и 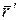, причем

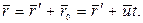(5.1)

В проекциях на оси координат векторное уравнение (5.1) записывается в виде, называемом преобразованиями Галилея:

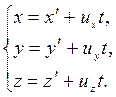(5.2)

В частном случае, когда система 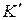движется со скоростью 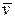вдоль положительного направления оси х системы К, преобразования координат Галилея имеют следующий вид:

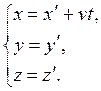
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета. Поэтому система уравнений (5.2) дополняется еще одним соотношением:

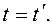(5.3)

Соотношения (5.2) – (5.3) справедливы лишь в случае 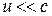. При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.

Продифференцируем уравнение (5.1) по времени и учитывая, что 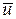=const, найдем соотношения между скоростями и ускорениями точки А относительно обеих систем отсчета:

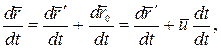
откуда

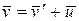, (5.4)

а также

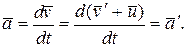(5.5)

Если на точку А другие тела не действуют, то 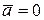и согласно (5.5) 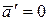, т.е. подвижная система К΄ является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.

Из выражения (5.5) следует, что

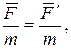или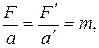

т.е. уравнения Ньютона (уравнения динамики) для материальной точки одинаковы во всех инерциальных системах отсчета или инвариантны по отношению к преобразованиям Галилея. Этот результат часто формулируют следующим образом: равномерное и прямолинейное движение системы как целого не влияет на ход протекающих в ней механических процессов.

Классическая механика Ньютона достоверно описывает движение макроскопических тел, движущихся со скоростями, намного меньшими скорости света. В конце XIX в. было установлено, что выводы классической механики противоречат некоторым опытным данным. В частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам Ньютона. Далее возникли затруднения при попытках применить классическую механику для объяснения распространения света. Согласно законам электродинамики скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и приблизительно равна с = 3·10⁸ м/с. Но в соответствии с законами классической физики скорость света может равняться с только в одной избранной системе отсчета. В любой другой системе отсчета, движущейся относительно избранной системы со скоростью v, она должна уже равняться c-v, или c+v. Это означает, что если справедлив закон сложения скоростей классической механики (формула (5.4)), то при переходе от одной инерциальной системы к другой законы электродинамики должны меняться, так как должна меняться скорость света. Таким образом, обнаружились противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности Галилея. Для преодоления возникших трудностей предлагались различные способы:

1. Принять несостоятельность принципа относительности применительно к электромагнитным явлениям. Еще со времен Фарадея электромагнитные явления рассматривались как процессы в особой, всепроникающей среде, заполняющей все пространство, - эфире. Согласно Х. Лоренцу инерциальная система отсчета, покоящаяся относительно эфира, - это особая система, в которой законы электродинамики Максвелла справедливы. Лишь в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.

2. Считать ошибочными уравнения электродинамики Максвелла и попытаться изменить их таким образом, чтобы они при переходе от одной инерциальной системы к другой (в соответствии с классическими представлениями о пространстве и времени) не менялись. Такая попытка, в частности, была предпринята Г. Герцем, который считал, что эфир полностью увлекается движущимися телами, поэтому электромагнитные явления протекают одинаково, независимо от того, покоится тело или движется. Принцип относительности справедлив.

3. Отказаться от классических представлений о пространстве и времени, с тем, чтобы сохранить и принцип относительности, и законы Максвелла. С этой точки зрения оказываются неточными не уравнения электромагнитного поля, а законы механики Ньютона, согласующиеся со старыми представлениями о пространстве и времени. Таким образом, изменять нужно законы классической механики, а не законы электродинамики Максвелла.

Вспомним, как трактовались пространство и время в классической физике. Пространство рассматривалось как бесконечная пустая протяженность, вмещающая в себе все тела и не зависящая от материи. Время рассматривалось как абсолютный фактор равномерного потока длительности, в котором все возникает и исчезает. При этом время не зависит ни от каких процессов в мире.

Развитие естествознания опровергло эти представления. Никакого абсолютного пространства и времени не существует. Вселенная заполнена материей в форме вещества и поля, а пространство выступает как всеобщее свойство материи. Время всегда связано с движением и развитием материи. Таким образом, пространство – это форма бытия материи, которая выражает ее протяженность и структурность; время – это форма бытия материи, характеризующая длительность существования всех объектов, полей и последовательность смены событий.

Основными свойствами пространства и времени являются: а) единство и неразрывная связь материи, пространства и времени; б) абсолютная непрерывность и относительная прерывность пространства и времени. Непрерывность проявляется в распространении материальных полей в пространстве всех тел и систем, в бесконечном следовании элементов длины при движении тела между двумя точками. Прерывность пространства относительна и проявляется в раздельном существовании материальных объектов и систем, каждая из которых имеет определенные размеры и границы. Прерывность времени характеризуется лишь временем существования качественных состояний материи, каждое из которых возникает и исчезает, переходя в другие формы; в) время обладает длительностью, однонаправленностью, необратимостью.

Последовательно развивая новые, отличные от классических, представления о пространстве и времени, А. Эйнштейн в начале XX в. создал специальную теорию относительности (СТО). В рамках этой теории удалось согласовать принцип относительности с электродинамикой Максвелла. При этом новая теория не отменяла старую (ньютоновскую механику), а включала ее в себя как частный, предельный случай.