Сумма геометрической прогрессии вида

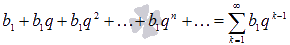
со знаменателем q является сходящимся числовым рядом, если 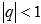, и расходящимся рядом при .

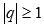Докажем это.

Мы знаем, что сумма первых n членов геометрической прогрессии находится по формуле

.

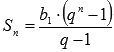При 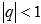справедливо

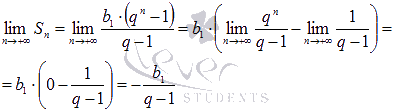
что указывает на сходимость числового ряда.

При q = 1 имеем числовой ряд

.

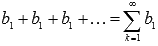Его частичные суммы находятся как

,

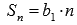а предел частичных сумм бесконечен

,

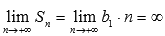что указывает на расходимость ряда в этом случае.

Если q = -1, то числовой ряд примет вид

.

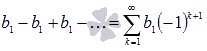Частичные суммы принимают значение 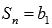для нечетных n, и 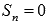для четных n. Из этого можно сделать вывод, что предел частичных сумм не существует и ряд расходится.

При 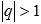справедливо

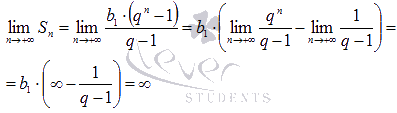
что указывает на расходимость числового ряда.

Обобщенно гармонический ряд 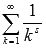сходится при s > 1 и расходится при .

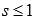Доказательство.

Для s = 1 получим гармонический ряд 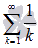, а выше мы установили его расходимость.

При s < 1 справедливо неравенство 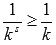для всех натуральных k. В силу расходимости гармонического ряда 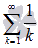можно утверждать, что последовательность его частичных сумм неограниченна (так как не существует конечного предела). Тогда последовательность частичных сумм числового ряда 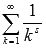тем более неограниченна (каждый член этого ряда больше соответствующего члена гармонического ряда), следовательно, обобщенно гармонический ряд расходится при s < 1.

Осталось доказать сходимость ряда 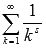при s > 1.

Запишем разность :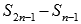

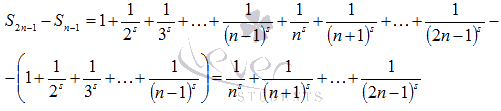
Очевидно, что

,

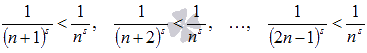тогда

Распишем полученное неравенство для n = 2, 4, 8, 16, …

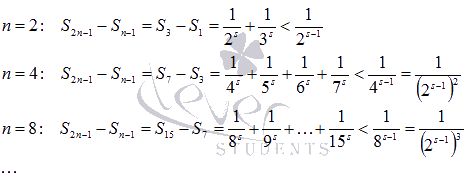
Используя эти результаты, с исходным числовым рядом можно провести следующие действия:

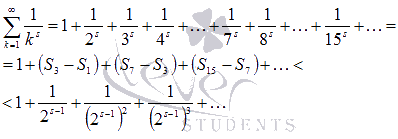
Выражение 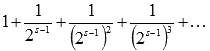представляет собой сумму геометрической прогрессии, знаменатель которой равен 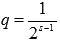. Так как мы рассматриваем случай при s > 1, то 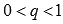. Поэтому

.

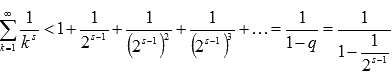Таким образом, последовательность частичных сумм обобщенно гармонического ряда при s > 1 является возрастающей и в тоже время ограниченной сверху значением 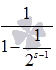, следовательно, она имеет предел, что указывает на сходимость ряда 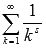. Доказательство завершено.

Числовой ряд 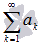называется знакоположительным, если все его члены положительны, то есть, .

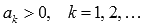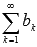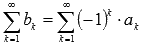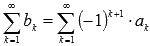Числовой ряд называется знакочередующимся, если знаки его соседних членов различны. Знакочередующийся числовой ряд можно записать в виде или , где .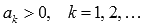

Числовой ряд 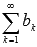называется знакопеременным, если он содержит бесконечное множество как положительных, так и отрицательных членов.

Знакочередующийся числовой ряд является частным случаем знакопеременного ряда.

Ряды

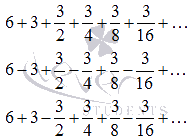
являются знакоположительным, знакочередующимся и знакопеременным соответственно.

Для знакопеременного ряда существует понятие абсолютной и условной сходимости.

Знакопеременный ряд 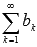называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов, то есть, сходится знакоположительный числовой ряд .

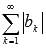К примеру, числовые ряды 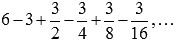и 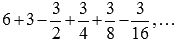абсолютно сходятся, так как сходится ряд 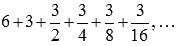, являющийся суммой бесконечно убывающей геометрической прогрессии.

Знакопеременный ряд 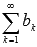называется условно сходящимся, если ряд 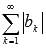расходится, а ряд 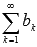сходится.

В качестве примера условно сходящегося числового ряда можно привести ряд 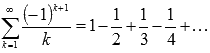. Числовой ряд 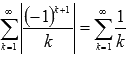, составленный из абсолютных величин членов исходного ряда, расходящийся, так как является гармоническим. В то же время, исходный ряд является сходящимся, что легко устанавливается с помощью признака Лейбница. Таким образом, числовой знакочередующийся ряд 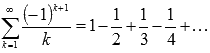условно сходящийся.