2015-01-07
775
Пусть мы имеем числовую последовательность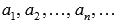 
, где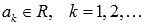 
.
Приведем пример числовой последовательности: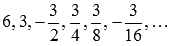 
.
Числовой ряд – это сумма членов числовой последовательности вида
.
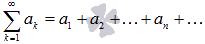В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: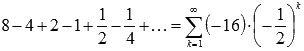 
.
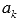называют общим членом числового ряда или k-ым членом ряда.
Для предыдущего примера общий член числового ряда имеет вид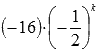 
.
Частичная сумма числового ряда – это сумма вида
,
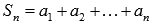где n – некоторое натуральное число.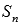 
называют также n-ой частичной суммой числового ряда.
К примеру, четвертая частичная сумма ряда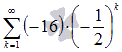 
есть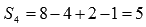 
.
Частичные суммы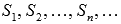 
образуют бесконечную последовательность частичных сумм числового ряда.
Для нашего ряда n –ая частичная сумма находится по формуле суммы первых n членов геометрической прогрессии
,
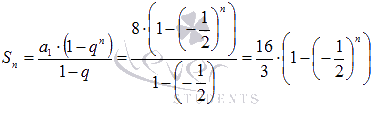то есть, будем иметь следующую последовательность частичных сумм: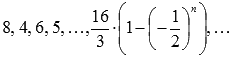 
.
Числовой ряд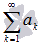 
называется сходящимся, если существует конечный предел последовательности частичных сумм 
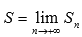. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд 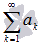называется расходящимся.
Суммой сходящегося числового ряда 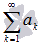называется предел последовательности его частичных сумм, то есть, 
.
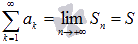В нашем примере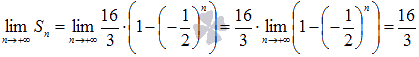 
, следовательно, ряд 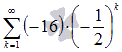сходится, причем его сумма равна шестнадцати третьим: 
.
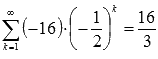В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица: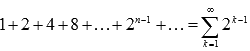 
. n-ая частичная сумма определяется выражением
,
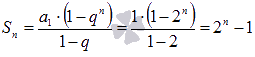а предел частичных сумм бесконечен:
.
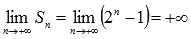Еще одним примером расходящегося числового ряда является сумма вида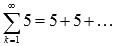 
. В этом случае n-ая частичная сумма может быть вычислена как
.
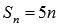Предел частичных сумм бесконечен
.
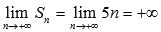Сумма вида
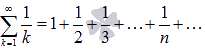
называется гармоническим числовым рядом.
Сумма вида
,
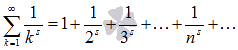где s – некоторое действительное число, называется обобщенно гармоническим числовым рядом.
Приведенных определений достаточно для обоснования следующих очень часто используемых утверждений, рекомендуем их запомнить.
Гармонический ряд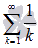 
является расходящимся.
Докажем расходимость гармонического ряда.
Предположим, что ряд сходится. Тогда существует конечный предел его частичных сумм. В этом случае можно записать
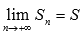и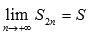 
,
что приводит нас к равенству
.
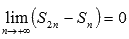С другой стороны,
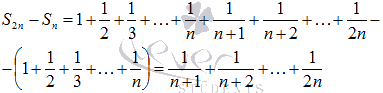
Не вызывают сомнения следующие неравенства
.
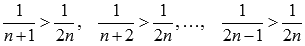Таким образом,
.
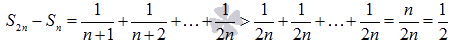Полученное неравенство
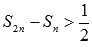
указывает нам на то, что равенство
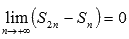
не может быть достигнуто, что противоречит нашему предположению о сходимости гармонического ряда.
Вывод: гармонический ряд расходится.
