· Расход жидкости в трубке тока:
а) объемный расход 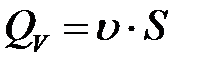 ;
;
б) массовый расход 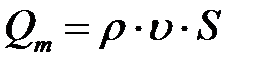 , где S – площадь поперечного сечения трубки тока; υ – скорость жидкости;
, где S – площадь поперечного сечения трубки тока; υ – скорость жидкости; 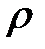 – ее плотность.
– ее плотность.
 · Уравнение неразрывности струи:
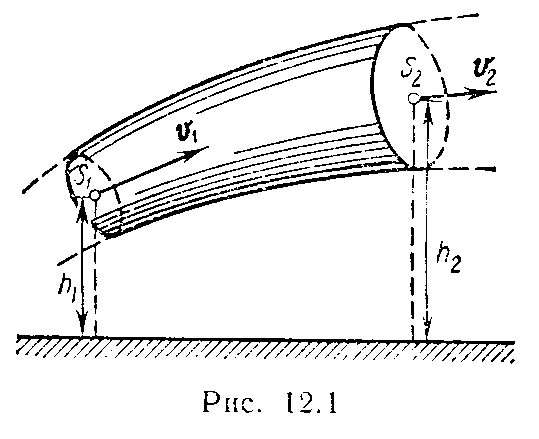
· Уравнение неразрывности струи:
 ,
,
где S 1 и S 2 – площади поперечного сечения трубки тока в двух местах; υ 1 и υ 2 –соответствующие скорости течений.
· Уравнение Бернулли для идеальной несжимаемой жидкости в общем случае
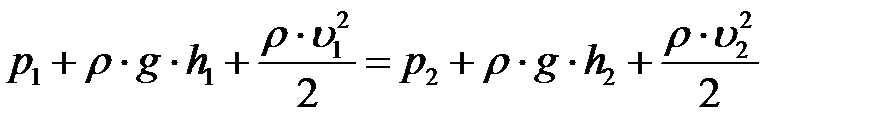 ,
,
где p 1 и p 2 – статические давления жидкости в двух сечениях трубки тока; υ 1 и υ 2 –скорости жидкости в этих сечениях; 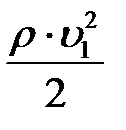 и
и 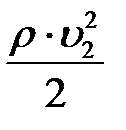 – динамические давления жидкости в этих же сечениях; h 1и h 2 – высоты их над некоторым уровнем;
– динамические давления жидкости в этих же сечениях; h 1и h 2 – высоты их над некоторым уровнем; 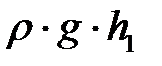 и
и 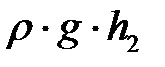 – гидростатические давления.
– гидростатические давления.
· Скорость течения жидкости из малого отверстия в открытом широком сосуде:
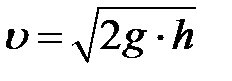 ,
,
где h— глубина, на которой находится отверстие относительно уровня жидкости в сосуде.
· Формула Пуазейля. Объем жидкости (газа), протекающей за время t через длинную трубку:
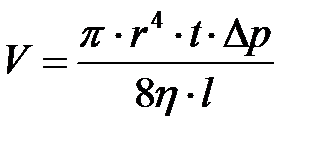 ,
,
где r — радиус трубки; l – ее длина; Δ p – разность давлений на концах трубки; η – динамическая вязкость (коэффициент внутреннего трения) жидкости.
|
|
|
· Число Рейнольдса для потока жидкости в длинных трубках:
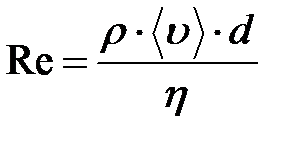 ,
,
где < υ > – средняя по сечению скорость течения жидкости; d – диаметр трубки,и для движения шарика в жидкости:
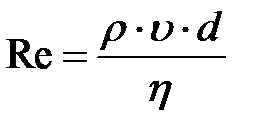 ,
,
где υ – скорость шарика; d— его диаметр.
Число Рейнольдса Re есть функция скорости v тела, линейной величины l, определяющей размеры тела, плотности 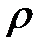 и динамической вязкости η жидкости, т. е.
и динамической вязкости η жидкости, т. е. 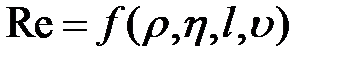 .
.
При малых значениях чисел Рейнольдса, меньших некоторого критического значения 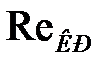 , движение жидкости является ламинарным. При значениях
, движение жидкости является ламинарным. При значениях 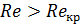 движение жидкости переходит в турбулентное.
движение жидкости переходит в турбулентное.
Критическое число Рейнольдса для движения шарика в жидкости 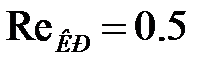 ; для потока жидкости в длинных трубках
; для потока жидкости в длинных трубках 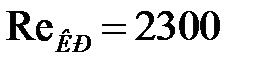 .
.
· Формула Стокса. Сила сопротивления F, действующаясо стороны потока жидкости на медленно движущийся в ней шарик:
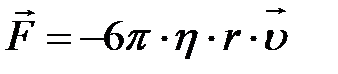 ,
,
где r – радиус шарика; υ – его скорость.
Формула справедлива для скоростей, при которых число Рейнольдса много меньше единицы (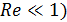 .
.
 2015-01-07
2015-01-07 873
873








