Решение задач. Пример 1. Даны две матрицы

Пример 1. Даны две матрицы:

А = 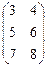, В = .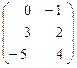

Найти матрицы: А + В, 2А – 4В.

Решение. Матрицы А и В можно складывать и вычитать, так как их размерности совпадают. По правилу сложения матриц:

А + В = = .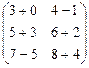

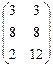По правилу вычитания матриц:

А - В = = .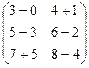

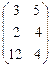Прежде, чем найти матрицу 2А – 4В, найдем матрицы 2А и –4В, воспользовавшись правилом умножения матрицы на скаляр:

2А = 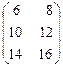- 4В = .

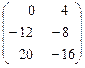Согласно правилу сложения матриц имеем

2А – 4В = =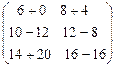

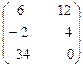
Матрицу 2А – 4В можно было искать как разность матриц 2А и 4В.

Пример 2. Даны матрицы

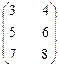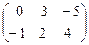А = , В = , C = .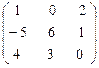

Указать все возможные произведения матриц и найти любые два. Запишем размерности матриц: А = (3 х 2), B = (2 x 3), C = (3 x 3). Можно найти А × B, B × C, C × A. Найдем АВ и ВС.

А × B = = = .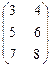

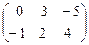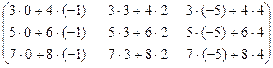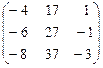Размерность матрицы произведения проверим по размерностям матриц А и В: (3 x 2) × (2 x 3) = (3 x 3)

В × С = =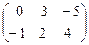

= =

= .

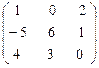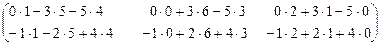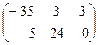Контроль: (2 х 3)× (3 х 3) = (2 х 3).

Пример 3. Найти все матрицы, перестановочные с матрицей А = .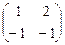

Решение. Пусть В = 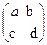. Найдем ее элементы

АВ = =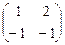

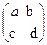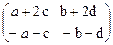
ВА = =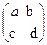

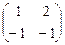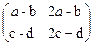
Так как АВ = ВА, то выполняются равенства

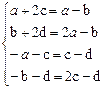Þ = .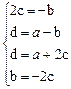

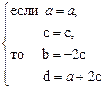Итак: В = 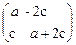, где а и с – любые числа.