Базисом n-мерного линейного пространства Vn называется любая упорядоченная система n линейно независимых векторов этого пространства.
1.6. Дать определение координат вектора 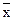 в базисе
в базисе 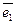 ,
, 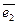 , …,
, …, 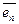 .
.
Теорема. Если 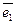 ,
, 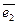 , …,
, …, 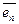 - базис линейного n-мерного пространства Vn, то любой вектор
- базис линейного n-мерного пространства Vn, то любой вектор 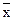 этого пространства можно представить как линейную комбинацию векторов
этого пространства можно представить как линейную комбинацию векторов 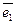 ,
, 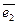 , …,
, …, 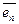 , то есть
, то есть
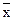 = a1
= a1 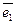 + a2
+ a2 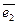 + … + an
+ … + an 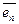 .
.
Последнее равенство называется разложением вектора 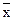 по базису
по базису 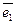 ,
, 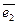 , …,
, …, 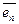 .
.
Коэффициенты 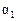 ,
, 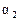 , …,
, …, 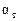 этого разложения определяются однозначно и называются координатами вектора
этого разложения определяются однозначно и называются координатами вектора 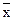 в базисе
в базисе 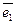 ,
, 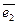 , …,
, …, 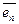 .
.
 2015-01-07
2015-01-07 288
288







