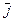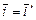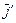Пример 1. Выяснить, является ли линейным векторным пространством множество R2 всех геометрических векторов, концы которых лежат в первой четверти системы координат.
Решение. Проверим выполнение операций сложения и умножения на число.
В результате сложения двух векторов мы получим вектор, конец которого тоже лежит в первой четверти. При умножении вектора на число a < 0 мы получим вектор, конец которого будет лежать в третьей четверти. Операция умножения на число не выполнена. Значит, данное векторное пространство не является линейным.
Пример 2. В базисе В = ( ,
,  ,
, 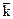 ) заданы векторы
) заданы векторы
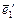 =
=  +
+  ,
, 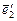 =
=  +
+ 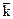 ,
, 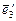 =
=  +
+ 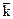 ,
, 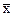 = -
= -  + 2
+ 2  +
+ 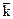 . Доказать, что система В¢ = (
. Доказать, что система В¢ = (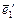 ,
, 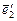 ,
, 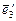 ) – базис и найти координаты вектора
) – базис и найти координаты вектора 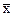 в базисе В¢.
в базисе В¢.
Решение. Выпишем координаты векторов 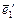 ,
, 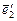 ,
, 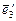 ,
, 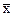 в исходном базисе В = (
в исходном базисе В = ( ,
,  ,
, 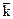 ) в виде матриц - столбцов:
) в виде матриц - столбцов:
Е¢1 = 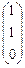 ; Е¢2 =
; Е¢2 = 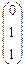 ; Е¢3 =
; Е¢3 = 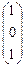 ; X =
; X = 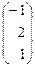 .
.
Убедимся, что векторы 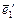 ,
, 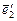 ,
, 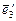 образуют базис. Составим матрицу А из координат этих векторов и найдем ее ранг.
образуют базис. Составим матрицу А из координат этих векторов и найдем ее ранг.
А = 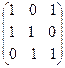 ~
~ 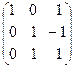 ~
~ 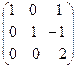 Þ ranq А = 3.
Þ ranq А = 3.
Ранг матрицы равен числу векторов, значит, эти векторы линейно независимы и образуют базис. Матрица А является матрицей перехода ТВ ® В¢ от базиса В к базису В¢ или матрицей линейного преобразования:
ТВ ® В¢ = 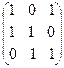 .
.
Запишем разложение вектора 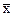 по базису В¢ в векторной и матричной формах:
по базису В¢ в векторной и матричной формах:
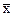 = a
= a 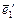 + b
+ b 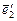 + g
+ g 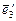 ,
,
X = ТВ ® В¢ ×X¢,
где X¢ = 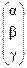 -матрица-столбец координат вектора
-матрица-столбец координат вектора 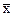 в базисе В¢.
в базисе В¢.
Находим искомую матрицу Х¢ с помощью обратного преобразования:
Х¢ = (ТВ ® В¢)-1 × X – формула преобразования координат при преобразовании базиса
Х¢ = 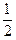
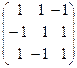 ×
× 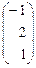 =
= 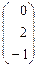 ,
,
то есть 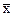 = 2
= 2 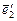 -
- 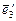 .
.
Пример 3. Даны два линейных преобразования:
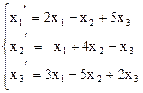 ,
, 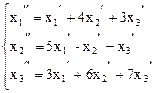
Найти линейное преобразование, выражающее вектор 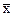 ² через вектор
² через вектор 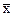 .
.
Решение. Запишем матрицы линейных преобразований:
Х¢ = 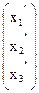 , A =
, A = 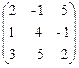 , X =
, X = 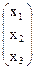 ,
,
X² = 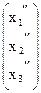 , B =
, B = 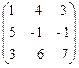 .
.
В матричной форме линейные преобразования запишутся так:
Х¢ = А Х, X² = B × X¢.
Подставим во второе равенство выражение Х¢ из первого, получим
X² = В × А × Х.
Матрица С = В × А будет являться матрицей искомого линейного преобразования
С = В × А = 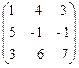
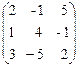 =
= 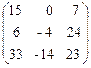 .
.
Следовательно, искомое преобразование таково:
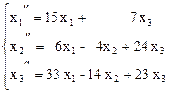 .
.
Пример 4. Найти матрицу перехода (матрицу линейного преобразования) ТВ®В¢, если базис В¢ = (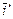 ,
, 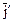 ) получен зеркальным отображением от вектора
) получен зеркальным отображением от вектора  базиса В = (
базиса В = ( ,
,  ).
).
Решение. Найдем координаты векторов 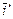 и
и 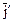 в базисе
в базисе
В = ( ,
,  ), (см. рисунок):
), (см. рисунок):
|
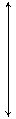
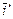 =
=  ,
, 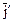 = -
= -  или
или 
|




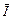 =
= 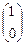 ,
, 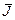 =
= 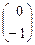 . ТВ®В¢ =
. ТВ®В¢ = 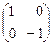 .
.
|
 2015-01-07
2015-01-07 5276
5276