Пример 1. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
A = 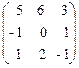 .
.
Решение. Напишем характеристическое уравнение данной матрицы А:
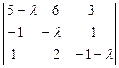 = 0.
= 0.
Разложим определитель по элементам первой строки:
(5 - l) 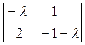 - 6
- 6 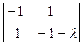 + 3
+ 3 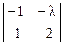 = 0.
= 0.
l3 - 4l2 - 4l + 16 = 0
l2 (l - 4) – 4 (l - 4) = 0.
(l - 4) (l2 – 4) = 0. Корни этого уравнения l1 = 4, l2 = 2, l3 = -2 являются собственными значениями линейного преобразования.
Для нахождения собственных векторов используем систему уравнений:
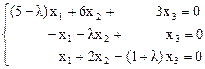
Эта система имеет множество ненулевых решений, так как ранг ее меньше 3. Полагая l = l1 = 4, получаем систему уравнений для нахождения первого собственного вектора 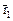 (х1, x2, x3):
(х1, x2, x3):
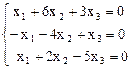 .
.
Ясно, что определитель основной матрицы этой системы равен нулю. Однако определитель 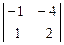 = 2 ¹ 0, поэтому первое уравнение системы можно отбросить:
= 2 ¹ 0, поэтому первое уравнение системы можно отбросить:
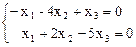 .
.
Последняя система решается так, как показано в примере 5 из темы 5:
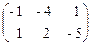 Þ х1: x2: x3 =
Þ х1: x2: x3 = 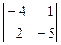 t:-
t:- 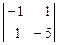 t:
t: 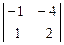 t =
t =
= 18 t: 4 t: 2 t = 9 t: -2 t: t.
Собственный вектор 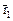 = t (9, -2, 1), t ¹ 0.
= t (9, -2, 1), t ¹ 0.
Полагая l = l2 = 2, получаем систему уравнений:
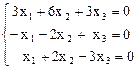 Þ
Þ 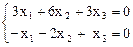 Þ
Þ 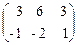 Þ
Þ
Þ х1: x2: x3 = 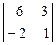 t: -
t: - 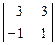 t:
t: 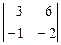 t =12 t: -6t:0 =
t =12 t: -6t:0 =
= 2 t: -t: 0. 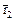 = t (2, -1, 0), t ¹ 0.
= t (2, -1, 0), t ¹ 0.
Полагая l = l3 = -2, получаем систему уравнений:
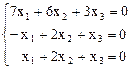 Þ
Þ 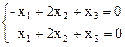 Þ
Þ 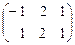 Þ
Þ
Þ х1: x2: x3 = 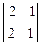 t: -
t: - 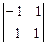 t:
t: 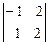 t = 0: 2 t: -4t = 0: t:-2t
t = 0: 2 t: -4t = 0: t:-2t
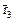 = t (0, 1, -2), t ¹ 0.
= t (0, 1, -2), t ¹ 0.
Собственные векторы линейно независимы, то есть их можно принять за базис.
Пример 2. Найти характеристические числа и собственные векторы матрицы
А = 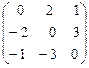 .
.
Решение. Запишем характеристическое уравнение матрицы А:
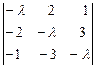 = 0.
= 0.
Разложим определитель по первой строке:
-l 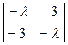 - 2
- 2 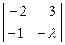 +
+ 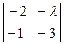 = 0
= 0
-l (l2 + 9) – 2 (2l + 3) + 6 - l = 0
-l3 – 14 l = 0
l (l2 + 14) = 0
l1 = 0 l2 = -14 l2,3 = ± 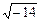 .
.
Корни этого уравнения l1 = 0, l2,3 = ± 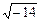 являются собственными значениями линейного преобразования.
являются собственными значениями линейного преобразования.
Для нахождения собственных векторов используем систему уравнений:
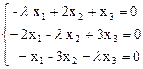
Эта система имеет множество ненулевых решений, так как ее ранг меньше 3.
Полагая l = l1 = 0, получаем систему уравнений для нахождения первого собственного вектора 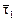 (х1, х2, x3):
(х1, х2, x3):
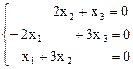 Þ
Þ 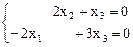 Û
Û 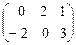 Þ
Þ
Þ х1: x2: x3 = 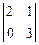 t: -
t: - 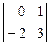 t:
t: 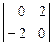 t = -6 t: - 2 t: 4 t =
t = -6 t: - 2 t: 4 t =
= 3 t: -t: 2 t. 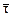 1 = t (3, -1, 2), t ¹ 0.
1 = t (3, -1, 2), t ¹ 0.
Полагая l = l2,3 = ± 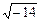 , получаем систему уравнений:
, получаем систему уравнений:
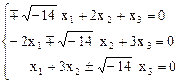 Þ
Þ 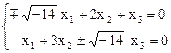 Þ
Þ
Þ 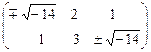 Þ х1: x2: x3 =
Þ х1: x2: x3 = 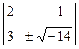 t: -
t: -
- 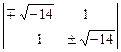 t:
t: 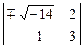 t = (-3 × ± 2
t = (-3 × ± 2 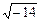 ) t:
) t:
- (14 – 1) t: (-2 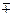 3
3 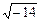 ) t = (3
) t = (3 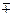 2
2 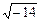 ) t: 13 t:(2 ± 3
) t: 13 t:(2 ± 3 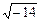 ) t
) t
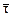 2,3 = t (3
2,3 = t (3 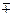 2
2 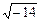 , 13, 2 ± 3
, 13, 2 ± 3 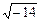 ), t ¹ 0.
), t ¹ 0.
Пример 3. Найти собственные значения и собственные векторы матрицы
А = 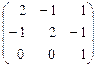 .
.
Решение. Запишем характеристическое уравнение заданной матрицы А:
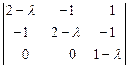 = 0.
= 0.
Разложим определитель по третьей строке:
(1 - l) 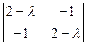 = 0
= 0
(1 - l) ((2 - l)2 – 1) = 0
(1 - l) (2 - l – 1) (2 - l + 1) = 0
(1 - l)2 (3 - l) = 0
l1,2 = 1 l3 = 3
Корни этого уравнения l1,2 = 1, l3 = 3 являются собственными значениями матрицы А.
Для нахождения ее собственных векторов используем систему:
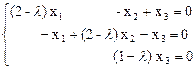
Эта система имеет множество ненулевых решений, так как ранг ее меньше 3.
Полагая l = l1,2 = 1, получим систему уравнений
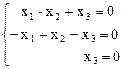 Þ
Þ 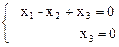 Û
Û 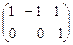 Þ
Þ
Þ х1: x2: x3 = 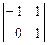 t: -
t: - 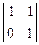 t:
t: 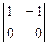 t = -t: - t:0.
t = -t: - t:0.
Собственный вектор 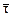 1,2 = t (1, 1, 0), t ¹ 0.
1,2 = t (1, 1, 0), t ¹ 0.
Полагая l = l3 = 3, получим систему уравнений:
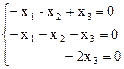 Û
Û 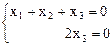 Þ
Þ 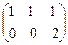 Þ
Þ
Þ х1: x2: x3 = 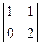 t: -
t: - 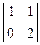 t:
t: 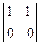 t = 2 t: - 2 t:0.
t = 2 t: - 2 t:0.
Собственный вектор 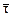 3 = t (1, -1, 0), t ¹ 0.
3 = t (1, -1, 0), t ¹ 0.
Пример 4. Методом собственных векторов привести к каноническому виду уравнение кривой второго порядка
17 х2 + 12 ху + 8 у2 = 20.
Решение. Квадратичная форма 17 х2 + 12 ху + 8 у2 полностью определяется матрицей А = 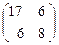 . Найдем собственные значения матрицы А. Запишем и решим характеристическое уравнение:
. Найдем собственные значения матрицы А. Запишем и решим характеристическое уравнение:
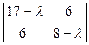 = 0.
= 0.
(17 - l) (8 - l) – 36 = 0 Þ l2 – 25 l + 100 = 0 Þ l1 = 5, l2 = 20. Квадратичная форма 17 х2 + 12 ху + 8 у2 преобразуется к каноническому виду l1 (х¢)2 + l2 (у¢)2, то есть 5 (х¢)2 + 20 (у¢)2, а данное уравнение кривой к виду: 5 (х¢)2 + 20 (у¢)2 = 20 или
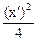 +
+ 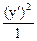 = 1. Данная кривая – эллипс.
= 1. Данная кривая – эллипс.
Пример 5. Определить тип кривой второго порядка
3х2 + 10 ху + 3у2 – 2х – 14 у – 13 = 0, написать ее каноническое уравнение и найти каноническую систему координат.
 2015-01-07
2015-01-07 483
483








