Выбора базиса ?

Теорема. Если линейное преобразование f в базисе

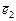, , …, имеет матрицу А и в базисе 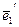, , …, 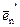- матрицу В, то

det (A - lE) = det (В - lE),

где l - любое действительное число, Е – единичная матрица порядка n.

Из этой теоремы вытекает, что характеристический многочлен det (A - lE) линейного преобразования f остается неизменным при переходе к новому базису, несмотря на то, что матрица линейного преобразования меняется. Следовательно, характеристическое уравнение не зависит от выбора базиса.