В задачах 1 – 6 найти собственные значения и собственные векторы линейных преобразований, заданных своими матрицами.
1. 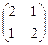 2.
2. 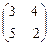 3.
3. 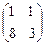 4.
4. 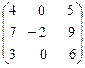
5. 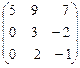 6.
6. 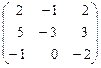 .
.
Ответ. 1. l1 = 1, 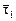 = t (1, -1); l2 = 3,
= t (1, -1); l2 = 3, 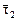 = t (1, 1), t ¹ 0.
= t (1, 1), t ¹ 0.
2. l1 = 7, 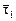 = t (1, 1); l2 = -2,
= t (1, 1); l2 = -2, 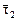 = t (4, -5), t ¹ 0.
= t (4, -5), t ¹ 0.
3. l1 = -1, 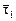 = t (1, -2); l2 = 5,
= t (1, -2); l2 = 5, 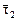 = t (1, 4), t ¹ 0.
= t (1, 4), t ¹ 0.
4. l1 = -2, 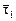 = t (0, 19, 0); l2 = 1,
= t (0, 19, 0); l2 = 1, 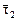 = t (15, 8, -9),
= t (15, 8, -9),
l3 = 9, 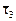 = t (11, 16, 11), t ¹ 0.
= t (11, 16, 11), t ¹ 0.
5. l1,2 = 1, 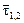 = t (-4, 1, 1), l3 =5,
= t (-4, 1, 1), l3 =5, 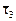 = t (1, 0, 0), t ¹0.
= t (1, 0, 0), t ¹0.
6. l1 = l2 = l3 = -1, 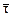 = t (1, 1, -1), t ¹0.
= t (1, 1, -1), t ¹0.
В задачах 7 – 10 методом собственных векторов привести к каноническому виду следующие уравнения кривой второго порядка.
7. 5 х2 + 8 ху + 5 у2 = 9
8. х2 - 2 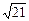 ху + 5 у2 = 24
ху + 5 у2 = 24
9. 5 х2 + 4 ху + 2 у2 = 18
10. 4 ху + 3 у2 = 36
Ответы. 7) l1 =1, l2 = 9; эллипс 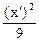 +
+ 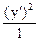 = 1.
= 1.
8) l1 =8, l2 = -2; гипербола 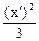 -
- 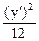 = 1.
= 1.
9) l1 =1, l2 = 6; эллипс 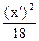 +
+ 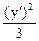 = 1.
= 1.
10) l1 =4, l2 = -1; гипербола 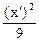 -
- 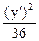 = 1.
= 1.
В задачах 11 – 13 определить тип кривой второго порядка, написать ее каноническое уравнение и найти каноническую систему координат.
11. х2 + 6 ху + у2 + 6х + 2у – 1 = 0.
12. х2 + 2 ху + у2 + 3х + у = 0.
13. 9х2 + 4 ху + 6 2 + 16х + 8у – 2 = 0.
Ответ. 11) l1 =4, l2 = -2; гипербола 4 (х¢)2 – 2 (у²)2 =1,
0¢ (0, -1), 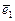 =
= 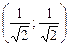 ,
, 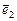 =
= 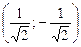 ; 12) l1 = 2, l2 = 0; парабола (х²)2 = -
; 12) l1 = 2, l2 = 0; парабола (х²)2 = - 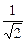 у², 0¢
у², 0¢ 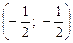 ,
, 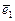 =
= 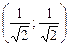 ,
,
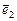 =
= 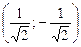 ; 13) l1 =5, l2 = 10; ‘эллипс
; 13) l1 =5, l2 = 10; ‘эллипс 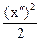 + (у²)2 = 1,
+ (у²)2 = 1,
0¢ 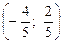 ,
, 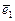 =
= 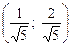 ,
, 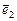 =
= 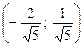 .
.
Варианты проверочных работ
Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей А.
1. А = 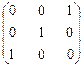 . Ответ. l1 = -1
. Ответ. l1 = -1 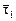 = t (-1, 0, 1)
= t (-1, 0, 1)
l2,3 = 1 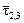 = t (1, k, 1), t ¹ 0.
= t (1, k, 1), t ¹ 0.
2. А = 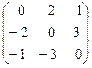 .
.
Ответ. l1 = 0 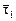 = t (3, -1, 2), t ¹ 0
= t (3, -1, 2), t ¹ 0
l2,3 = ± 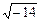 .
.
3. А = 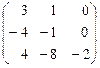 .
.
Ответ. l1 = -2 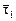 = t (0, 0, 1)
= t (0, 0, 1)
l2,3 = 1 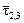 = t (3, -6, 20), t ¹ 0.
= t (3, -6, 20), t ¹ 0.
4. А = 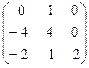 .
.
Ответ. l1,2,3 = 2 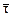 = t (1, 2, k), t ¹ 0.
= t (1, 2, k), t ¹ 0.
5. А = 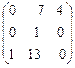 .
.
Ответ. l1 = 1 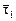 = t (-59, 3, -20)
= t (-59, 3, -20)
l2 = 2 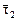 = t (2, 0, 1)
= t (2, 0, 1)
l3 = -2 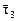 = t (2, 0, -1), t ¹ 0.
= t (2, 0, -1), t ¹ 0.
6. А = 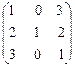 .
.
Ответ. l1 = 1 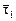 = t (0, 1, 0)
= t (0, 1, 0)
l2 = -2 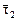 = t (-1, 0, 1)
= t (-1, 0, 1)
l3 = 4 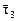 = t (3, 4, 3), t ¹ 0.
= t (3, 4, 3), t ¹ 0.
7. А = 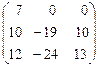 .
.
Ответ. l1 = 7 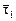 = t (7, 5, 6)
= t (7, 5, 6)
l2 = 1 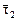 = t (0, 1, 2)
= t (0, 1, 2)
l3 = -7 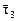 = t (0, -5, 6), t ¹ 0.
= t (0, -5, 6), t ¹ 0.
8. А = 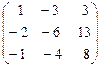 .
.
Ответ. l1,2,3 = 1 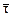 = t (3, 1, 1), t ¹ 0.
= t (3, 1, 1), t ¹ 0.
9. А = 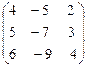 .
.
Ответ. l1,2 = 0 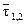 = t (1, 2, 3)
= t (1, 2, 3)
l3 = 1 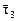 = t (1, 1, 1), t ¹ 0.
= t (1, 1, 1), t ¹ 0.
10. А = 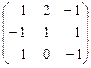 .
.
Ответ. l1 = 0 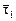 = t (1, 0, 1)
= t (1, 0, 1)
l2 = 0 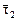 = t (1, 2, 3)
= t (1, 2, 3)
l3 = -1 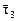 = t (4, -1, 6), t ¹ 0.
= t (4, -1, 6), t ¹ 0.
2. Определить тип кривой второго порядка.
1. 3х2 + 3у2 – 4ху + 4х + 4у + 1 = 0.
Ответ. l1 = 1, l2 = 5, эллипс.
2. х2 + у2 – 4ху + 2х + 4у + 1 = 0.
Ответ. l1 = 3, l2 = -1, гипербола.
3. 5х2 – 6ух + 5у2 – 2х + 3у - 32 = 0.
Ответ. l1 = 8, l2 = 2, эллипс.
4. 9 х2 – 24 ху + 16 у2 – 3х + 4 = 0.
Ответ. l1 = 0, l2 = 25, парабола.
5. 3х2 + 3у2 + 10 ху - 2х - 14у - 13 = 0.
Ответ. l1 = 8, l2 = -2, гипербола.
6. 7х2 + 4 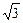 ху + 3у2 + х – у = 0.
ху + 3у2 + х – у = 0.
Ответ. l1 = 1, l2 = 9, эллипс.
7. х2 – 4 ух + 4у2 – 4х – 3у – 7 = 0.
Ответ. l1 = 0, l2 = 5, парабола.
8. 2х2 + 4ху + 5у2 – 6х – 8у = 1.
Ответ. l1 = 1, l2 = 6, эллипс.
9. 5х2 + 12 ху – 22 х – 12 у – 19 = 0.
Ответ. Ответ. l1 = 9, l2 = -4, гипербола
10. х2 – 2ху + у2 – 10 х – 6у + 25 = 0.
Ответ. l1 = 0, l2 = 2, парабола.
 2015-01-07
2015-01-07 975
975







