2015-01-07
2234
Говорят, что дискретная случайная величина X распределена по биномиальному закону, если возможные значения этой случайной величины 0, 1, 2,…, n, а вероятность каждого из значений определяется по формуле Бернулли
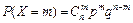, (21)
где 0 £ p £ 1; q = 1 – p; m = 0, 1, 2,…, n.
Постоянные p и n, входящие в формулу (21), называются параметрами биномиального распределения.
На практике биномиальное распределения возникает при следующих условиях: пусть производится серия из n независимых испытаний, в каждом из которых событие A может осуществиться с вероятностью p. Тогда случайная величина X, определяющая число появлений события A в серии из n испытаний, распределена по биномиальному закону.
Закон называется «биномиальным» потому, что правую часть равенства (21) можно рассматривать как общий член разложения бинома Ньютона:
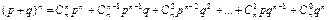. (22)
Ряд распределения случайной величины X, распределенной по биномиальному закону, имеет вид:
| xi | … | k | … | n – 1 | n | ||
| pi | qn | npqn -1 | … | Cnkpkqn - k | … | npn -1 q | pn |
Для случайной величины, распределенной по биномиальному закону,
M [ X ] = np, D [ X ] = npq,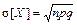 
. (23)
Пример 30 По каналу связи передается 5 сообщений. Каждое сообщение с вероятностью 0,1 независимо от других искажается. Случайная величина X – число искаженных сообщений. Построить ряд распределения этой случайной величины, вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение непосредственно по ряду распределения и сравнить со значениями, которые получаются при использовании формул (23). Найти вероятность того, что будет искажено не более одного сообщения.
Решение. Условие задачи соответствует проведению n = 5 независимых испытаний, в каждом из которых с вероятностью p = 0,1 может осуществиться событие A = {искажение передаваемого сигнала}. Случайная величина X, обозначающая число искаженных сообщений, распределена по биномиальному закону. Возможные значения этой случайной величины: 0, 1, 2, 3, 4, 5. Вероятности возможных значений случайной величины определяются по формуле Бернулли:
; 
;
; 
;
; 
.
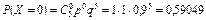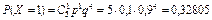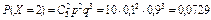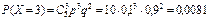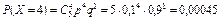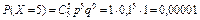Ряд распределения имеет вид:
| xi | Итого | ||||||
| pi | 0,59049 | 0,32805 | 0,0729 | 0,0081 | 0,00045 | 0,00001 | |
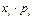| 0,32805 | 0,1458 | 0,0243 | 0,0018 | 0,00005 | 0,5 | |
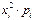| 0,32805 | 0,2916 | 0,0729 | 0,0072 | 0,00025 | 0,7 |
Убедимся, что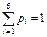 
.
Вычислим числовые характеристики данной случайной величины:
;
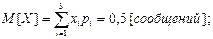
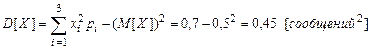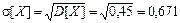[ сообщений ];
xmod = 0 [ сообщений ].
Вычислим числовые характеристики этой случайной величины по формулам (23):
M [ X ] = n p = 5 × 0,1 = 0,5; D [ X ] = n p q = 5 × 0,1 × 0,9 = 0,45.
Как и следовало ожидать, получены точно такие же значения.
Вероятность того, что будет искажено не более одного сообщения,
P (X £ 1) = P (X = 0) + P (X = 1) = 0,59049 + 0,32805 = 0,91854.
