На практике геометрическое распределение возникает при следующих условиях: пусть производится серия независимых опытов, в каждом из которых может произойти событие А с одной и той же вероятностью p. Опыты продолжаются до первого появления события А. Тогда случайная величина X, определяющая число неудач, предшествующих успеху, распределена по геометрическому закону.
Возможные значения этой случайной величины: 0, 1, 2, …, n, …, а вероятность каждого из этих значений определяется по формуле
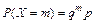 , (24)
, (24)
где 0 £ p £ 1; q = 1 – p; m = 0, 1, 2, …, n, ….
Геометрическое распределение зависит от параметра p.
Замечание – Геометрическая прогрессия – это числовая последовательность a 1, a 2,…, an,…, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему, умноженному на одно и то же, не равное нулю, число, называемое знаменателем геометрической прогрессии q,
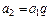 ,
, 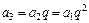 , …,
, …, 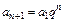 .
.
Сумма бесконечно убывающей (q < 1) геометрической прогрессии 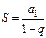 .
.
Условие 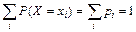 выполняется, так как принимая во внимание условие сходимости геометрического ряда
выполняется, так как принимая во внимание условие сходимости геометрического ряда 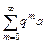 , (
, (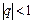 ) и формулу
) и формулу 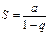 для его суммы, получаем
для его суммы, получаем 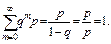
Ряд распределения случайной величины X, имеющей геометрический закон:
| xi | … | m | … | n | … | |||
| pi | p | q1 p | q2 p | … | qm p | … | qn p | … |
Для случайной величины, распределенной по геометрическому закону,
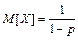 ,
, 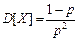 ,
, 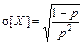 ,
, 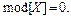
Пример 31 Вероятность изготовления нестандартного изделия при некотором технологическом процессе равна 0,06. Контролер берет из партии изделие и сразу проверяет его качество. Если оно оказывается нестандартным, то дальнейшие испытания прекращаются, а партия задерживается. Если же изделие оказывается стандартным, то контролер проверяет следующее изделие и т. д. Записать закон распределения случайной величины X – числа стандартных изделий, проверенных до выявления брака.
Решение. Условие задачи соответствует проведению независимых испытаний, в каждом из которых с вероятностью p = 0,06 может осуществиться событие A = {обнаружено нестандартное изделие}. В этом случае неудача – обнаружение стандартного изделия, успех – обнаружение нестандартного изделия. Случайная величина X – число стандартных изделий, проверенных до выявления брака, распределена по геометрическому закону. Возможные значения этой случайной величины: 0, 1, 2, 3, …, m, …. По условию p = 0,06, q = 1 – 0,06 = 0,94.
Вероятности значений определяются по формуле (24):
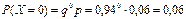 (то есть нестандартное изделие будет обнаружено сразу же при проверке первого изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 0);
(то есть нестандартное изделие будет обнаружено сразу же при проверке первого изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 0);
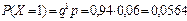 (то есть нестандартное изделие будет обнаружено при проверке второго изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 1);
(то есть нестандартное изделие будет обнаружено при проверке второго изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 1);
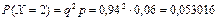 (то есть нестандартное изделие будет обнаружено при проверке третьего изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 2) и т. д.
(то есть нестандартное изделие будет обнаружено при проверке третьего изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 2) и т. д.
Закон распределения можно записать в виде 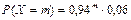 , или в виде ряда распределения случайной величины X:
, или в виде ряда распределения случайной величины X:
| xi | … | m | … | n | … | |||
| pi | 0,06 | 0,0564 | 0,053016 | … | 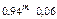 | … | 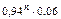 | … |
В литературе встречается и иное определение геометрического распределения: случайная величина X распределена по геометрическому закону, если эта величина дискретна и определяет число независимых испытаний Бернулли, предшествующих первому появлению успеха. Возможные значения этой случайной величины 1, 2, …, n, …, а вероятность каждого из значений определяется по формуле
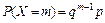 , (25)
, (25)
где 0 £ p £ 1; q = 1 – p; m = 1, 2,…, n,….
В этом примере случайная величина X определяет число произведенных опытов, предшествующих успеху.
Ряд распределения случайной величины X, распределенной по геометрическому закону, имеет вид:
| xi | … | m | … | n | … | ||
| pi | p | q 1 p | … | qm -1 p | … | qn -1 p | … |
Для случайной величины, распределенной по геометрическому закону,
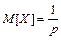 ,
, 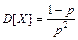 ,
, 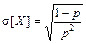 ,
, 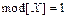 .
.
Пример 32 На основании данных примера 31 з аписать закон распределения случайной величины X – числа проверенных изделий до выявления брака.
Решение. Условие задачи соответствует проведению независимых испытаний, в каждом из которых с вероятностью p = 0,06 может осуществиться событие A = {обнаружено нестандартное изделие}. В этом случае неудача – обнаружение стандартного изделия, успех – обнаружение нестандартного изделия. Случайная величина X – число проверенных изделий до выявления брака, распределена по геометрическому закону. Возможные значения этой случайной величины: 1, 2, 3, …, m,…. По условию p = 0,06, q = 0,94.
Вероятности возможных значений определяются по формуле (25):
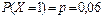 (то есть нестандартное изделие будет обнаружено сразу же при проверке первого изделия и партию задержат);
(то есть нестандартное изделие будет обнаружено сразу же при проверке первого изделия и партию задержат);
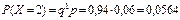 (то есть нестандартное изделие будет обнаружено при проверке второго изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 1);
(то есть нестандартное изделие будет обнаружено при проверке второго изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 1);
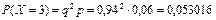 (то есть нестандартное изделие будет обнаружено при проверке третьего изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 2) и т. д.
(то есть нестандартное изделие будет обнаружено при проверке третьего изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 2) и т. д.
Закон распределения рассмотренной случайной величины можно записать в виде 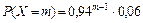 , или в виде ряда распределения случайной величины X:
, или в виде ряда распределения случайной величины X:
| xi | … | m | … | n | … | |||
| pi | 0,06 | 0,0564 | 0,053016 | … | 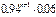 | … | 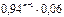 | … |
Пример 33 Производится подбрасывание игрального кубика до первого выпадения шести очков. Какова вероятность того, что первое выпадение шестерки произойдет при втором подбрасывании игрального кубика?
Решение. Условие задачи соответствует проведению независимых испытаний, в каждом из которых с вероятностью p = 1/6 может осуществиться событие A = {выпадение шести очков}. В этом случае неудача – выпадение любого числа от 1 до 5, успех – выпадение шести очков. Случайная величина X – число подбрасываний игрального кубика до выпадения шестерки, распределена по геометрическому закону. Возможные значения этой случайной величины: 1, 2, 3, …, m,…. Вероятность успеха p = 1/6, вероятность неудачи q = (1 – 1/6) = 5/6.
Вероятности появления шестерки при втором подбрасывании кубика определим по формуле (25):
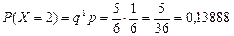 (то есть шестерка появится при втором подбрасывании кубика, при этом при первом подбрасывании появится любое число от 1 до 5).
(то есть шестерка появится при втором подбрасывании кубика, при этом при первом подбрасывании появится любое число от 1 до 5).
Закон распределения рассмотренной случайной величины можно записать в виде 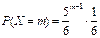 .
.
 2015-01-07
2015-01-07 7777
7777
