Задание 8. Для определенной в условии задачи дискретной случайной величины

Для определенной в условии задачи дискретной случайной величины:

1) построить ряд распределения и столбцовую диаграмму;

2) найти функцию распределения и построить ее график;

3) вычислить числовые характеристики: математическое ожидание, моду, дисперсию, среднее квадратическое отклонение.

8.1–8.5. Вероятность того, что банк предоставит кредит каждому из клиентов, равна . 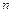клиентов собираются обратиться в один из банков города с просьбой предоставить кредит. Случайная величина X – число клиентов, получивших кредит.

№ варианта	n	p
		0,4
		0,6
		0,8
		0,7
		0,6

8.6–8.10. Имея в запасе n патронов, стрелок производит выстрелы в мишень до первого попадания, или пока не израсходует все патроны. Вероятность попадания при каждом выстреле равна p. Случайная величина X – число выстрелов, произведенных в мишень.

№ варианта	n	p
		0,8
		0,6
		0,8
		0,75
		0,6

8.11–8.15. Производится n выстрелов по мишени. Вероятность попадания при первом выстреле равна p, и после каждого произведенного выстрела она уменьшается на 0,1. Случайная величина X – число попаданий в мишень.

№ варианта	n	p
		0,7
		0,6
		0,8
		0,7
		0,4

8.16–8.20. Вероятность возвращения кредита в установленный договором срок для каждого клиента равна 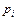. Случайная величина X – число кредитов, возвращенных в срок тремя клиентами.

№ варианта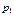
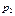
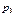
	0,8	0,6	0,8
	0,8	0,6	0,6
	0,7	0,8	0,7
	0,50	0,6	0,8
	0,5	0,8	0,6

8.21–8.25. Вероятность выигрыша по одному билету лотереи равна . Случайная величина X – число выигрышных билетов среди 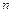купленных.

№ варианта	n	p
		0,06
		0,05
		0,08
		0,1
		0,04

8.26–8.30. Имеются 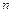ключей, из которых только один подходит к замку. Наудачу выбирается ключ и делается попытка открыть им дверь, если ключ не подходит, то этот ключ в последующих опробованиях не участвует. Случайная величина Х – число проб при открывании замка.