Закон распределения непрерывной случайной величины задан функцией плотности распределения вероятностей f (x). Требуется:
1) определить значение параметра C;
2) построить график функции плотности распределения вероятностей;
3) найти функцию распределения данной случайной величины и построить ее график;
4) вычислить числовые характеристики данной случайной величины: математическое ожидание, моду, медиану, дисперсию, среднее квадратическое отклонение;
5) найти вероятность того, что данная случайная величина примет значение, принадлежащее отрезку [ a; b ].
| 9.1. | 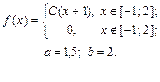
| 9.2. | 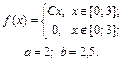
| |
| 9.3. | 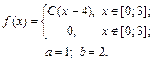
| 9.4. | 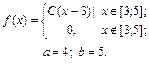
| |
| 9.5. | 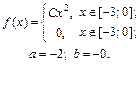
| 9.6. | 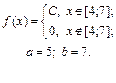
| |
| 9.7. | 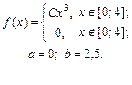
| 9.8. | 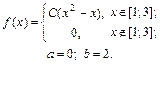
| |
| 9.9. | 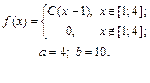
| 9.10. | 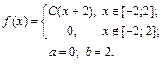
| |
| 9.11. | 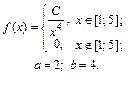
| 9.12. | 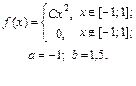
| |
| 9.13. | 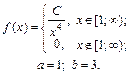
| 9.14. | 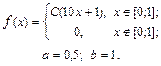
| |
| 9.15. | 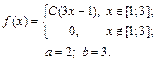
| 9.16. | 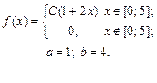
| |
| 9.17. | 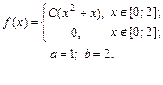
| 9.18. | 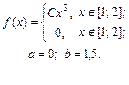
| |
| 9.19. | 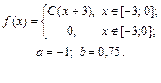
| 9.20. | 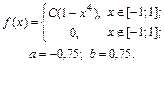
| |
| 9.21. | 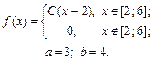
| 9.22. | 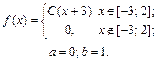
| |
| 9.23. | 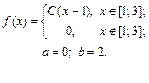
| 9.24. | 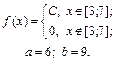
| |
| 9.25. | 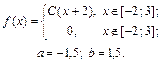
| 9.26. | 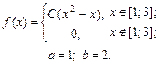
| |
| 9.27. | 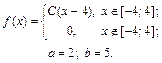
| 9.28. | 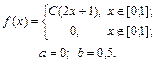
| |
| 9.29. | 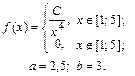
| 9.30. | 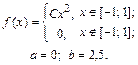
|
 2015-01-07
2015-01-07 353
353








