10.1–10.5. Поток заявок, поступающих на станцию технического обслуживания автомобилей, представляет собой простейший поток событий. Известно, что в течение некоторого промежутка времени среднее число заявок, поступающих за одни сутки (24 часа), равно 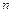 . Для этого промежутка времени найти вероятность того, что за один час поступит:
. Для этого промежутка времени найти вероятность того, что за один час поступит:
а) не менее  заявок;
заявок;
б) более  заявок.
заявок.
| № варианта | n | k |
10.6–10.10. Поток заявок, поступающих на телефонную станцию, представляет собой простейший поток событий. Известно, что в течение некоторого промежутка времени среднее число вызовов, поступающих за один час, равно 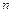 . Для этого промежутка времени найти вероятность того, что за одну минуту поступит не менее
. Для этого промежутка времени найти вероятность того, что за одну минуту поступит не менее  вызовов.
вызовов.
| № варианта | n | k |
10.11–10.15. Все значения равномерно распределенной случайной величины X принадлежат отрезку 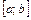 . Найти математическое ожидание, дисперсию и вероятность попадания значения случайной величины X в отрезок
. Найти математическое ожидание, дисперсию и вероятность попадания значения случайной величины X в отрезок 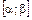 . Построить график плотности распределения случайной величины X.
. Построить график плотности распределения случайной величины X.
| № варианта | 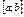 | 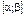 |
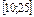 | 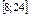 | |
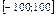 | 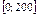 | |
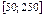 | 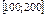 | |
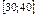 | 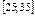 | |
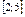 | 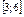 |
10.16–10.20. Троллейбусы данного маршрута идут с интервалом в 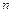 мин. Пассажир подходит к троллейбусной остановке в случайный момент времени. Какова вероятность появления пассажира не позднее чем за 2 мин до отхода следующего троллейбуса?
мин. Пассажир подходит к троллейбусной остановке в случайный момент времени. Какова вероятность появления пассажира не позднее чем за 2 мин до отхода следующего троллейбуса?
| № варианта | n |
10.21–10.25. Случайная величина Х – время безотказной работы воздушного фильтра автомобиля, распределена по показательному закону с математическим ожиданием 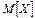 , (число лет). Определить дисперсию и вероятность того, что случайная величина Х примет значения в интервале
, (число лет). Определить дисперсию и вероятность того, что случайная величина Х примет значения в интервале 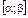 . Построить график плотности распределения случайной величины X.
. Построить график плотности распределения случайной величины X.
| № варианта | 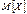 , (число лет) , (число лет) | 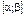 |
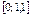 | ||
| 1,2 | 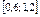 | |
| 1,1 | 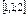 | |
| 0,8 | 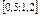 | |
| 0,9 | 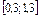 |
10.26–10.30. Время пользования Интернетом в вечернее время распределено по показательному закону с математическим ожиданием, равным 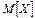 , часов. Найти вероятность того, что пользователь будет находиться в Интернете более
, часов. Найти вероятность того, что пользователь будет находиться в Интернете более 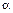 часов. Найти среднее квадратическое отклонение времени пользования Интернетом. Построить график плотности распределения случайной величины X.
часов. Найти среднее квадратическое отклонение времени пользования Интернетом. Построить график плотности распределения случайной величины X.
| № варианта | 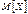 , ч , ч | 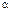 |
| 0,6 | 0,3 | |
| 0,8 | 0,1 | |
| 0,9 | 0,5 | |
| 1,0 | 0,6 | |
| 0,75 | 0,2 |
 2015-01-07
2015-01-07 1184
1184








