Метод замены переменной в неопределенном интеграле

Пример 5

Найти неопределенный интеграл.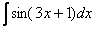

Для решения интеграла нам приглянулась табличная формула 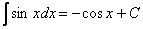, и всё дело хотелось бы свести к ней.

Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.

В данном случае напрашивается: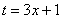

Вторая по популярности буква для замены – это буква .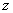

В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.

Итак: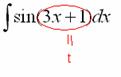

Но при замене у нас остаётся 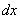! Если осуществляется переход к новой переменной 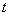, то в новом интеграле всё должно быть выражено через букву 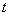, и дифференциалу 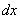там совсем не место.

Следует логичный вывод, что 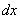нужно превратить в некоторое выражение, которое зависит только от.

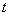Действие следующее. После того, как мы подобрали замену, в данном примере, 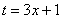, нам нужно найти дифференциал .

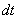Так как 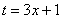, то

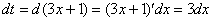
Т.е.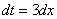

Теперь по правилам пропорции выражаем нужный нам :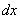

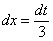
В итоге: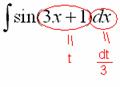

Таким образом:

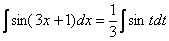
А это уже самый что ни на есть табличный интеграл 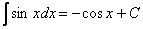(таблица интегралов, естественно, справедлива и для переменной ).

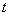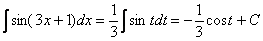
В заключении осталось провести обратную замену. Вспоминаем, что .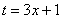

Чистовое оформление рассмотренного примера должно выглядеть примерно так:

“

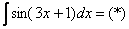
Проведем замену: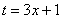

“

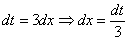
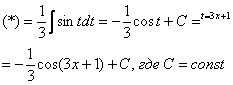
Значок не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.

Также всем рекомендую использовать математический знак вместо фразы «из этого следует это». И коротко, и удобно.

А теперь самое время вспомнить первый способ решения:

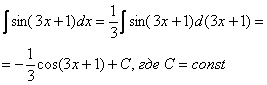
В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче.

Пример 6

Найти неопределенный интеграл.

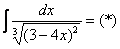
Проведем замену: 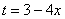(другую замену здесь трудно придумать)

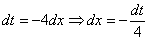
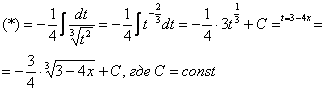
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.