Пусть функция u=f (x, y, z) определена и непрерывна в ограниченной замкнутой области T пространства Oxyz. Разобьем область T произвольным образом на n областей V 1, V 2,…, Vn, которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке 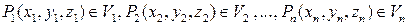 , которые назовем точками пунктуации. Обозначим через
, которые назовем точками пунктуации. Обозначим через 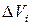 объем, а через
объем, а через 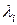 диаметр i- ойэлементарной области (i= 1,…, n),
диаметр i- ойэлементарной области (i= 1,…, n), 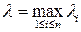 . Составим выражение
. Составим выражение
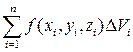 , (7)
, (7)
которое называется интегральной суммой Римана для функции u=f (x, y, z) по области T. Заметим, что выражение (7) зависит от способа разбиения области T на элементарные области и от способа выбора точек пунктуации.
Если существует предел выражения (7) при 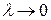 и если этот предел не зависит ни от способа разбиения области T на элементарные области, ни от способа выбора точек пунктуации, то он называется тройным интегралом от функции u=f (x, y, z) по области T и обозначается
и если этот предел не зависит ни от способа разбиения области T на элементарные области, ни от способа выбора точек пунктуации, то он называется тройным интегралом от функции u=f (x, y, z) по области T и обозначается
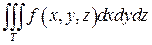
Таким образом,
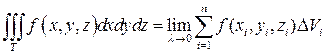 (8)
(8)
Свойства тройных интегралов аналогичны свойствам двойных интегралов.
Вычисление тройных интегралов сводится к вычислению повторных интегралов следующим образом. Пусть область T ограничена снизу поверхностью 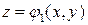 , сверху поверхностью
, сверху поверхностью 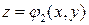 и с боков прямой цилиндрической поверхностью; проекцией области T на плоскость Oxy является область D (рис. 6). Такую область назовем правильной в направлении оси Oz.
и с боков прямой цилиндрической поверхностью; проекцией области T на плоскость Oxy является область D (рис. 6). Такую область назовем правильной в направлении оси Oz.
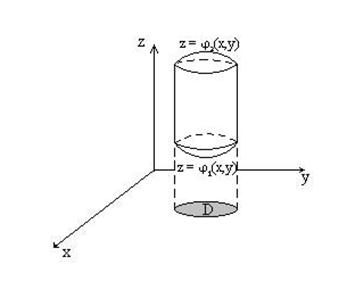
Рис. 6
Пусть функция u=f (x, y, z) определена и интегрируема в области T и для любых точек 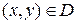 существует интеграл
существует интеграл
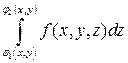 .
.
Тогда существует интеграл
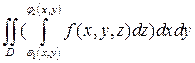
и справедлива формула
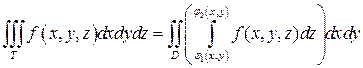 (9)
(9)
Аналогичные формулы справедливы и в случае, когда область T правильная в направлении оси Ox или оси Oy.
Теорема (о замене переменных в тройном интеграле). Пусть выполняются следующие условия:
1) функции x=x (u, v, w), y=y (u, v, w) и z=z (u, v, w) таковы, что каждой точке с координатами (x, y, z) из области T соответствует единственная точка с координатами (u, v, w) из области T 1 и наоборот;
2) функции x=x (u, v, w), y=y (u, v, w) и z=z (u, v, w) имеют непрерывные частные производные по переменным u, v и w;
3) функция u=f (x, y, z) определена и интегрируема в области T.
Тогда справедлива формула:
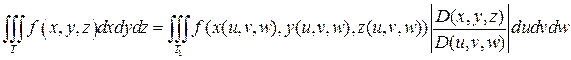 , (10)
, (10)
где
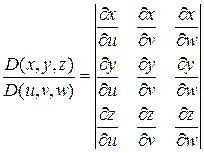
- якобиан перехода от декартовых координат к криволинейным координатам.
Частным случаем криволинейных координат для тройного интеграла являются цилиндрические и сферические координаты.
1) В случае цилиндрических координат положение точки M в пространстве определяется тремя числами 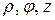 , где
, где 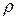 и
и 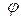 - полярные координаты проекции точки M на координатную плоскость Oxy, z – аппликата точки M (рис.7).
- полярные координаты проекции точки M на координатную плоскость Oxy, z – аппликата точки M (рис.7).
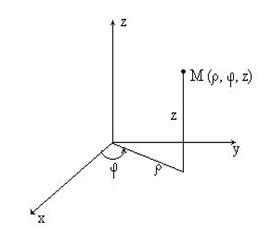
Рис. 7
Имеют место формулы:
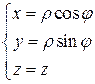 ,
,
якобиан перехода от декартовых координат к цилиндрическим равен 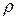 и формула (10) принимает вид:
и формула (10) принимает вид:
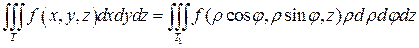 (11)
(11)
2) В случае сферических координат положение точки M в пространстве определяется тремя числами 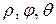 , где
, где 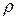 - расстояние от начала координат до точки M,
- расстояние от начала координат до точки M, 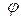 - угол между проекцией радиус-вектора точки M на плоскость Oxy и осью Ox,
- угол между проекцией радиус-вектора точки M на плоскость Oxy и осью Ox, 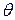 - угол между радиус-вектором точки M и осью Oz (рис.8).
- угол между радиус-вектором точки M и осью Oz (рис.8).
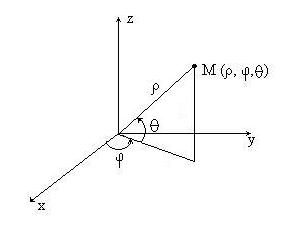
Рис. 8
Имеют место формулы:
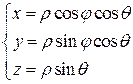 ,
,
якобиан перехода от декартовых координат к сферическим равен 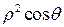 и формула (10) принимает вид:
и формула (10) принимает вид:
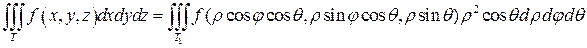 (12)
(12)
Задание 1. Вычислить интеграл:

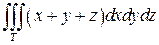 ,
,
где T - тетраэдр, ограниченный плоскостями: x+y+z =1, x= 0, y= 0, z= 0.
Решение. Изобразим область интегрирования (рис.9).
Область интегрирования ограничена снизу плоскостью z= 0, сверху плоскостью z= 1 -x-y, по бокам плоскостями x= 0 и y= 0. Проекцией области T на плоскость Oxy является область D - треугольник OAB. По формуле (9) имеем:
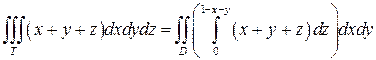 .
.
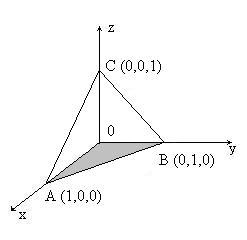
Рис. 9
Записывая двойной интеграл по области D через повторный интеграл, получим:
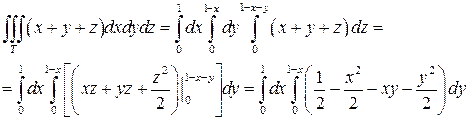
И, наконец, вычислим полученный повторный интеграл:
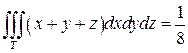 .
.
Задание 2. Перейдя к цилиндрическим координатам, вычислить интеграл:
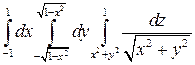 .
.
Решение. Изобразим область интегрирования (рис.10).
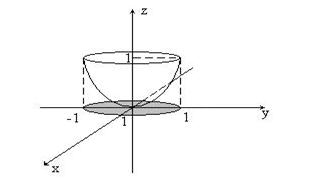
Рис. 10
Положим
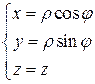
и применим формулу (11). Так как 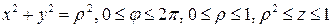 , то
, то 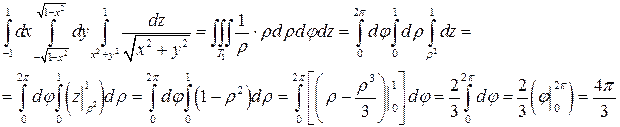
Задание 3. Переходя к сферическим координатам, вычислить интеграл:
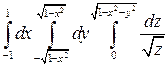 .
.
Решение. Область интегрирования T есть полушар 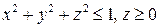 (рис.11).
(рис.11).
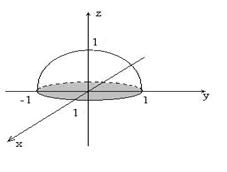
Рис. 11
Найдем пределы изменения сферических координат для области T 1:
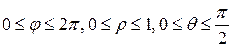
Следовательно, по формуле (12) имеем:
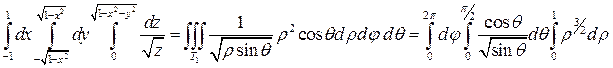 .
.
Вычислив полученный тройной интеграл, получим:
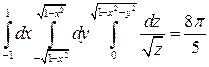 .
.
Приложения кратных интегралов
1. Геометрические приложения двойных интегралов
Площадь S плоской области (фигуры) D выражается в зависимости от рассматриваемой системы координат, следующими интегралами:
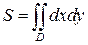 (13)
(13)
- в декартовых координатах,
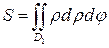 (14)
(14)
- в полярных координатах.
Пусть гладкая поверхность задана уравнением z=f (x, y). Тогда площадь части этой поверхности, проектирующейся в область D плоскости Oxy, равна:
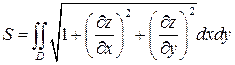 (15)
(15)
Пусть область T ограничена снизу плоскостью z= 0, сверху – непрерывной поверхностью z=f (x, y) и с боков прямой цилиндрической поверхностью. Если проекцией области T на плоскость Oxy является область D, то объем V области T выражается интегралом
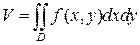 (16)
(16)
2. Механические приложения двойных интегралов.
Масса M пластинки, занимающей область D плоскости Oxy, имеющей плотность 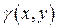 , равна:
, равна:
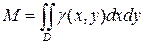 . (17)
. (17)
Статические моменты Mx и My этойпластинки относительно осей Ox и Oy
выражаются интегралами:
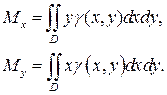 (18)
(18)
Координаты центра масс 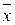 и
и 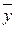 пластинки определяются следующим образом:
пластинки определяются следующим образом:
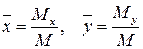 . (19)
. (19)
Моменты инерции пластинки относительно осей Ox и Oy соответственно равны:
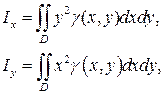 (20)
(20)
а момент инерции пластинки относительно начала координат равен:
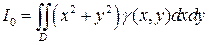 . (21)
. (21)
Заметим, что если рассматриваемая пластина однородна, то в приведенных формулах следует положить 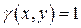 .
.
3. Геометрические приложения тройного интеграла
Объем V пространственной области T равен:
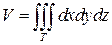 (22)
(22)
4.Механические приложения тройных интегралов. Масса M тела с плотностью 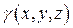 ,занимающего область T, равна
,занимающего область T, равна
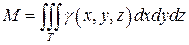 (23)
(23)
Статические моменты Mxy, Mxz, Myz тела относительно координатных плоскостей выражаются интегралами:
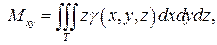
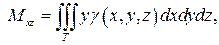 (24)
(24)
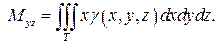
Координаты центра масс тела T определяются следующим образом:
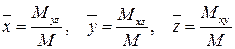 . (25)
. (25)
Моменты инерции тела относительно осей координат соответственно равны:
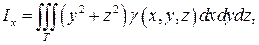
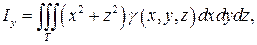 (26)
(26)
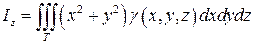 .
.
Заметим, что если рассматриваемое тело однородно, то в приведенных формулах следует положить 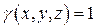 .
.
Задание 1. Найти объем тела, ограниченного поверхностями:
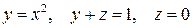 .
.
Решение. Данное тело ограничено снизу плоскостью z= 0, сверху плоскостью y+z= 1 и с боков цилиндром 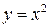 (рис.12а).
(рис.12а).
Проекцией рассматриваемого тела является область D (рис. 12б).
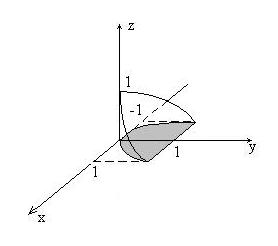
Рис. 12а
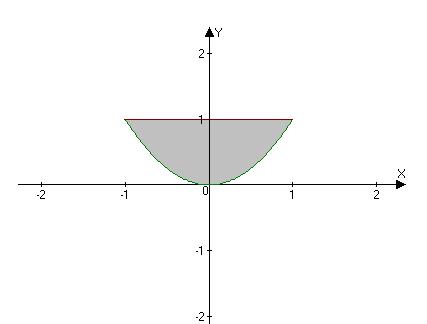
Рис. 12б
Найдем объем нашего тела двумя способами:
1) с помощью двойного интеграла;
2) с помощью тройного интеграла.
В первом случае воспользуемся формулой (16). В нашем случае f (x, y)=1 -y.
Следовательно,
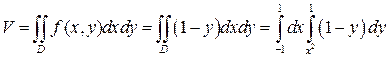 .
.
Вычисляем полученный повторный интеграл:
V= 8/15.
Теперь найдем значение объема данного тела с помощью тройного интеграла. Для этого воспользуемся формулой (22). Имеем:
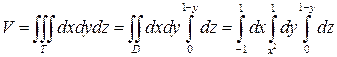 .
.
Вычисляем полученный тройной интеграл:
V= 8/15.
Задание 2. Найти координаты центра масс однородного тела, ограниченного поверхностями 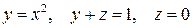 .
.
Решение. Данное тело изображено на рис.12а. Чтобы найти координаты центра масс рассматриваемого тела, воспользуемся формулами (25).
Найдем сначала массу тела. Для этого применим формулу (23) при 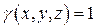 , так как наше тело однородное. Имеем:
, так как наше тело однородное. Имеем:
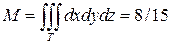
(это интеграл мы вычисляли в предыдущем примере).
Вычислим теперь статические моменты Mxy, Mxz, Myz рассматриваемого тела относительно координатных плоскостей. Для этого воспользуемся формулами (24) при 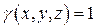 . Имеем:
. Имеем:
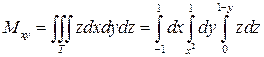 ,
,
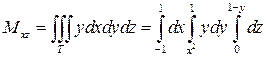 ,
,
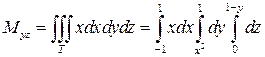
Вычислив полученные тройные интегралы, имеем:
Mxy= 16/105,
Mxz= 24/105,
Myz= 0.
Следовательно, координаты центра масс данного тела равны:
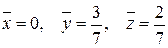 .
.
 2015-01-21
2015-01-21 5796
5796
