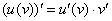
Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функция 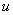 называется внешней функцией, а функция
называется внешней функцией, а функция 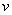 – внутренней (или вложенной) функцией.
– внутренней (или вложенной) функцией.
Пример 1
Найти производную функции 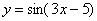
Под синусом у нас находится не просто буква «икс», а целое выражение 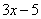 , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
, поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя: 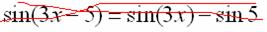
В данном примере уже из моих объяснений интуитивно понятно, что функция 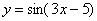 – это сложная функция, причем многочлен
– это сложная функция, причем многочлен 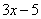 является внутренней функцией (вложением), а
является внутренней функцией (вложением), а 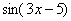 – внешней функцией.
– внешней функцией.
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.
В случае простых примеров вроде 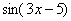 понятно, что под синус вложен многочлен
понятно, что под синус вложен многочлен 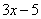 . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней?
. А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней?
Представим, что нам нужно вычислить на калькуляторе значение выражения 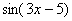 при
при 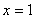 (вместо единицы может быть любое число).
(вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: 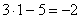 , поэтому многочлен
, поэтому многочлен 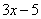 и будет внутренней функцией
и будет внутренней функцией 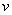 :
:
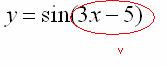 Во вторую очередь нужно будет найти
Во вторую очередь нужно будет найти 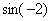 , поэтому синус – будет внешней функцией:
, поэтому синус – будет внешней функцией: 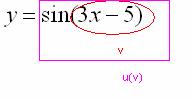 применяем правило дифференцирования сложной функции
применяем правило дифференцирования сложной функции 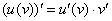 .
.
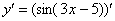
Сначала находим производную внешней функции 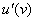 (синуса), смотрим на таблицу производных элементарных функций и замечаем, что
(синуса), смотрим на таблицу производных элементарных функций и замечаем, что 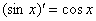 . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
. Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
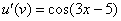
Обратите внимание, что внутренняя функция 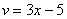 не изменилась, её мы не трогаем.
не изменилась, её мы не трогаем.
Ну и совершенно очевидно, что 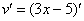
Результат применения формулы 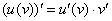 в чистовом оформлении выглядит так:
в чистовом оформлении выглядит так:
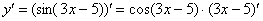
Далее мы берем производную внутренней функции, она очень простая:
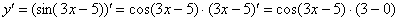
Постоянный множитель обычно выносят в начало выражения:
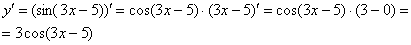
 2015-01-07
2015-01-07 1332
1332
