Пусть функции  определены на дуге MN кривой L. Разобьем дугу MN произвольным образом на n частей точками M=A 0, A 1,…, An = N,где Ai = Ai (xi, yi,zi), i= 0,1,…, n. Полученные дуги Ai -1 Ai, i= 1,…, n назовем элементарными дугами. В каждой из них произвольным образом выберем по точке
определены на дуге MN кривой L. Разобьем дугу MN произвольным образом на n частей точками M=A 0, A 1,…, An = N,где Ai = Ai (xi, yi,zi), i= 0,1,…, n. Полученные дуги Ai -1 Ai, i= 1,…, n назовем элементарными дугами. В каждой из них произвольным образом выберем по точке 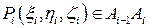 , i= 1,…, n, которые назовем точками пунктуации. Введем обозначения:
, i= 1,…, n, которые назовем точками пунктуации. Введем обозначения:

и составим выражение
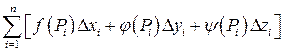 , (27)
, (27)
которое называется интегральной суммой Римана для данных функцийпо дуге MN. Заметим, что выражение (27) зависит от способа разбиения дуги MN на элементарные дуги и от способа выбора точек пунктуации.
Если существует предел выражения (27) при 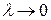 и если этот предел не зависит ни от способа разбиения дуги MN на элементарные дуги, ни от способа выбора точек пунктуации, то он называется криволинейным интегралом 2-го рода по дуге MN и обозначается
и если этот предел не зависит ни от способа разбиения дуги MN на элементарные дуги, ни от способа выбора точек пунктуации, то он называется криволинейным интегралом 2-го рода по дуге MN и обозначается
 .
.
Следовательно, по определению

 (28)
(28)
Свойства криволинейных интегралов 2-го рода аналогичны свойствам определенных интегралов.
Теорема (о вычислении криволинейных интегралов 2-го рода). Пусть даны параметрические уравнения дуги MN:
 ,
,
где  и пусть функции x (t), y (t), z (t) имеют непрерывные производные. Тогда:
и пусть функции x (t), y (t), z (t) имеют непрерывные производные. Тогда:
 (29)
(29) 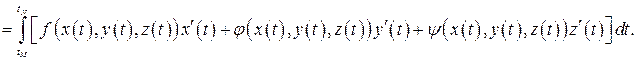
Задание 1. Вычислить интеграл

где линия L - отрезок O A с концами в точкахO(0,0,0), A (3,6,9).
Решение. Составим параметрические уравнения отрезка O A:
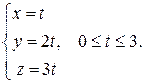
Тогда по формуле (29) имеем:
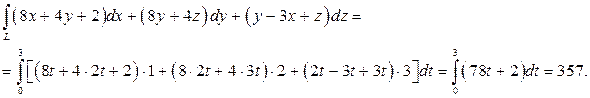
1. 5. Поверхностные интегралы (1-го рода)
Пусть функция u=f (x, y, z) определена и непрерывна на поверхности S пространства Oxyz. Разобьем поверхность S произвольным образом на n частей: S 1, S 2,…, Sn, которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке  , которые назовем точками пунктуации. Обозначим через
, которые назовем точками пунктуации. Обозначим через 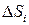 , i= 1,…, n площадь i- ой элементарной области,
, i= 1,…, n площадь i- ой элементарной области,  . Составим выражение
. Составим выражение
 , (30)
, (30)
которое называется интегральной суммой Римана для функции u=f (x, y, z) по поверхности S. Заметим, что выражение (30) зависит от способа разбиения поверхности S на элементарные области и от способа выбора точек пунктуации.
Если существует предел выражения (30) при 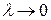 и если этот предел не зависит ни от способа разбиения поверхности S на элементарные области, ни от способа выбора точек пунктуации, то он называется поверхностным интегралом 1-го рода от функции
и если этот предел не зависит ни от способа разбиения поверхности S на элементарные области, ни от способа выбора точек пунктуации, то он называется поверхностным интегралом 1-го рода от функции  u=f (x, y, z) по поверхности S иобозначается
u=f (x, y, z) по поверхности S иобозначается
 .
.
Таким образом,
 (31)
(31)
Свойства поверхностных интегралов 1-го рода аналогичны свойствам двойных интегралов.
Теорема (о вычислении поверхностных интегралов 1- го рода).
Пусть поверхность S задана в явном виде уравнением  , где
, где 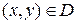 , D - областьплоскости Oxy и пусть функция
, D - областьплоскости Oxy и пусть функция  имеет непрерывные частные производные первого порядка. Тогда справедлива формула:
имеет непрерывные частные производные первого порядка. Тогда справедлива формула:
 (32)
(32)
Задание 1. Вычислить интеграл
 ,
,
где S - полусфера, задаваемая уравнением  .
.
Решение. Рассматриваемая поверхность S задана в явном виде:  , где
, где 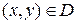 - круг радиуса R= 1 (рис.11). Для вычисления данного интеграла воспользуемся формулой (32). Имеем:
- круг радиуса R= 1 (рис.11). Для вычисления данного интеграла воспользуемся формулой (32). Имеем:
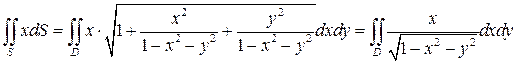
Перейдем в полученном двойном интеграле к полярной системе координат:

Так как значение первого интеграла  , то и весь интеграл равен нулю.
, то и весь интеграл равен нулю.
 2015-01-21
2015-01-21 1659
1659








