Сходимость или расходимость положительного ряда часто устанавливается путем сравнения его с другим рядом, заведомо сходящимся или расходящимся. В основе такого сравнения лежит следующая простая
Теорема 1. Пусть даны два положительных ряда
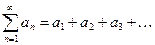
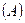
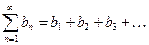
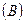
Если, хотя бы с некоторого места (скажем, для 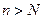 ), выполняется неравенство:
), выполняется неравенство: 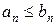 , то из сходимости ряда
, то из сходимости ряда 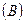 вытекает сходимость ряда
вытекает сходимость ряда 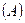 или – что то же – из расходимости ряда
или – что то же – из расходимости ряда 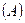 следует расходимость ряда
следует расходимость ряда 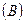 .
.
Иногда на практике более удобна следующая теорема, вытекающая из первой:
Теорема 2. Предположим, что 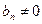 . Если существует предел
. Если существует предел
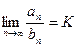 ,
,
то при 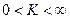 оба ряда сходятся или расходятся одновременно.
оба ряда сходятся или расходятся одновременно.
Наконец, приведем еще одну теорему сравнения, также представляющую собой следствие первой.
Теорема 3. Если, хотя бы с некоторого места (скажем, для 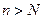 ), выполняется неравенство
), выполняется неравенство
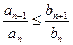 ,
,
то из сходимости ряда 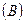 вытекает сходимость ряда
вытекает сходимость ряда 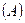 или – что то же – из расходимости ряда
или – что то же – из расходимости ряда 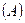 следует расходимость ряда
следует расходимость ряда 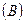 .
.
Пример 1. Рассмотрим ряд 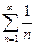 и сравним его с расходящимся рядом
и сравним его с расходящимся рядом 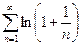 . Так как
. Так как 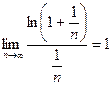 , то по Теореме сравнения 2 ряд
, то по Теореме сравнения 2 ряд 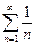 расходится.
расходится.
Рассмотрим ряд 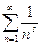 , где
, где 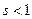 . Так как при таком ограничении на параметр
. Так как при таком ограничении на параметр 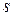 для всех
для всех 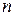 имеет место неравенство
имеет место неравенство 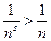 , а ряд
, а ряд 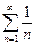 расходится, то по Теореме сравнения 1 ряд
расходится, то по Теореме сравнения 1 ряд 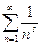 также будет расходящимся при
также будет расходящимся при 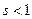 .
.
Рассмотрим ряд 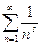 , где
, где 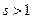 . Представим
. Представим 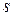 в виде
в виде 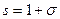 , где
, где 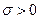 , и рассмотрим ряд
, и рассмотрим ряд 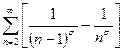 , который заведомо сходится. Так как
, который заведомо сходится. Так как 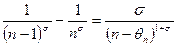
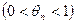 , то при
, то при 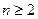
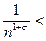
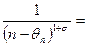
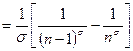 , откуда, по Теореме сравнения 1, и вытекает сходимость ряда
, откуда, по Теореме сравнения 1, и вытекает сходимость ряда 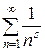 при
при 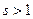 .
.
Ряд вида 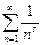 называется гармоническим. Таким образом, гармонический ряд сходится при
называется гармоническим. Таким образом, гармонический ряд сходится при 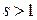 и расходится при
и расходится при 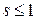 .
.
 2015-01-13
2015-01-13 1583
1583
