Признаки Коши и Даламбера получаются в результате сравнения положительного ряда
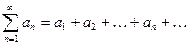
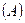
с геометрической прогрессией
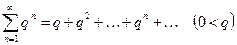 .
.
Признак Коши. Составим для ряда 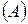 последовательность
последовательность 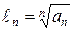 . Допустим, что последовательность
. Допустим, что последовательность 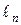 имеет предел
имеет предел 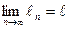 . Тогда при
. Тогда при 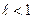 ряд сходится, а при
ряд сходится, а при 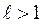 ряд расходится.
ряд расходится.
Замечание1. В случае, когда 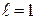 , этот признак не дает возможности судить о поведении ряда. Действительно, для рядов
, этот признак не дает возможности судить о поведении ряда. Действительно, для рядов 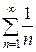 и
и 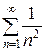 число
число 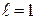 . Вместе с тем, первый ряд расходится, а второй сходится.
. Вместе с тем, первый ряд расходится, а второй сходится.
Если сравнение ряда 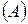 производить с геометрической прогрессией по Теореме 3, то мы придем к такому признаку:
производить с геометрической прогрессией по Теореме 3, то мы придем к такому признаку:
Признак Даламбера. Рассмотрим для ряда 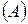 последовательность
последовательность
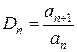 .
.
Допустим, что последовательность 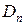 имеет предел
имеет предел 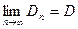 . Тогда при
. Тогда при 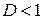 ряд сходится, а при
ряд сходится, а при 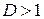 расходится.
расходится.
Замечание2. Как показывают те же примеры рядов 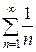 и
и 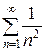 этот признак также ничего не дает, когда
этот признак также ничего не дает, когда 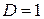 .
.
 2015-01-13
2015-01-13 518
518








