2015-01-13
1055
Мы видели в предыдущих пунктах, что в отношении положительных рядов сходимость можно установить благодаря наличию целого ряда признаков. Поэтому естественно начать с тех случаев, когда вопрос о сходимости данного ряда приводится к вопросу о сходимости положительного ряда.
Теорема1. Пусть дан ряд
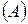
с членами произвольных знаков. Если сходится ряд
, 
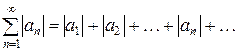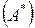
составленный из абсолютных величин его членов, то и данный ряд также сходится.
Определение 1. Если ряд 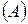сходится вместе с рядом 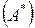, составленным из абсолютных величин его членов, то про ряд 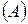говорят, что он абсолютно сходится.
По Теореме 1 одной сходимости ряда 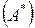уже достаточно для абсолютной сходимости ряда .
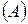Определение 2. Если ряд 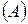сходится, а ряд 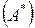– нет, то ряд 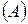называют условно (неабсолютно) сходящимся.
Для установления абсолютной сходимости ряда 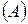к положительному ряду 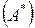могут быть применены все признаки сходимости положительных рядов, изученные ранее. Но нужно быть осторожным с признаками расходимости: если даже ряд 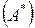окажется расходящимся, то ряд 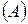может все же сходиться. Исключение представляют только признаки Коши и Даламбера, и именно потому, что когда они констатируют расходимость ряда 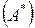, то это значит, что общий член 
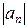ряда 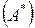не стремится к нулю, а тогда и 
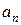к нулю не стремится, так что и ряд 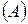также расходится.
Признак Даламбера. Пусть для последовательности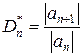 
существует 
;
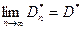тогда при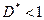 
данный ряд 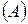абсолютно сходится, а при 
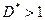он расходится.
Признак Коши. Пусть для последовательности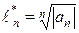 
существует
;
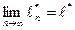тогда при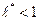 
данный ряд 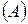абсолютно сходится, а при 
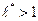он расходится.
