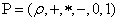 поле скаляров, множество
поле скаляров, множество 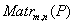 матриц порядка
матриц порядка 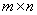
Определение. Квадратная матрица 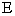 порядка
порядка 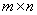 называется единичной матрицей
называется единичной матрицей 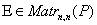 ,
, 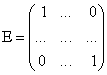
Пусть 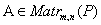 ,
, 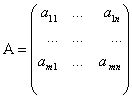
Теорема 1
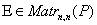 , то для
, то для 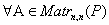 выполняется
выполняется 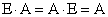
Доказательство:

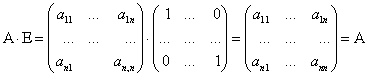
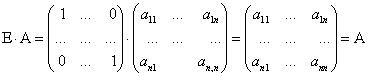
Из этого следует 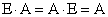 . Матрица
. Матрица 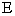 является единичной матрицей. Она выполняет роль единицы при умножении матриц.
является единичной матрицей. Она выполняет роль единицы при умножении матриц.
Определение. Квадратная матрица 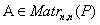 называется обратимой если существует
называется обратимой если существует 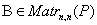 так, что выполняются условия
так, что выполняются условия 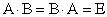
Матрица 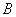 называется обратной к
называется обратной к 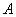 и обозначается
и обозначается 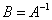 , тогда если
, тогда если 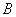 -это обратная к
-это обратная к 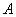 , то
, то 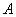 обратная к
обратная к 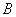
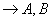 -это взаимообратные матрицы т.е.
-это взаимообратные матрицы т.е. 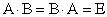
Теорема 2
Если 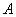 -обратима, то существует только одна матрица обратная к
-обратима, то существует только одна матрица обратная к 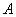
Доказательство:
 Пусть дана матрица
Пусть дана матрица 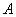 , которая обратима и пусть существуют матрицы
, которая обратима и пусть существуют матрицы 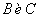 обратные к
обратные к 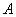 т.е.
т.е. 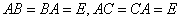 . Имеем
. Имеем 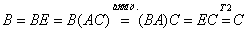
Обозначение: Множество всех обратимых матриц порядка 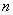 над полем
над полем 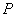 обозначается
обозначается 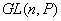
Теорема 3
Справедливы утверждения:
1) 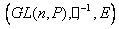 алгебра
алгебра
2) 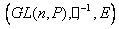 группа
группа
Доказательство:
 1)
1) 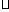 -это бинарная операция
-это бинарная операция
а) Пусть 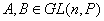 , так как
, так как 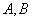 -обратимые матрицы, проверим, что
-обратимые матрицы, проверим, что 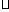 -это бинарная операция:
-это бинарная операция:
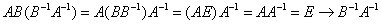 обратные к
обратные к 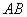
Аналогично: 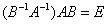 ,
, 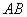 обратимая матрица т.е
обратимая матрица т.е 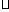 -это бинарная операция
-это бинарная операция
б) 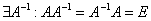 , матрица
, матрица 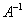 обратима, поэтому
обратима, поэтому 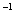 -это унарная операция
-это унарная операция
в) 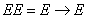 обратима т.е
обратима т.е 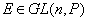
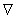 2) Докажем второе утверждение, что
2) Докажем второе утверждение, что 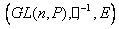 группа. Для этого проверим аксиомы групп:
группа. Для этого проверим аксиомы групп:
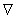 1)
1) 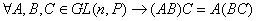
2) 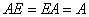
3) 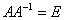
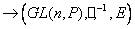 группа
группа
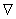
Следствие:
Произведение обратимых матриц есть обратимая матрица
Если 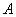 обратима, то
обратима, то 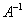 обратима
обратима
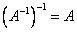
 2015-01-13
2015-01-13 6992
6992
