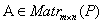 ,
, 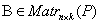
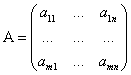 ,
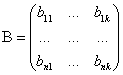
, 
Опр. Произведением 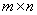 матрицы
матрицы  на
на 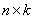 матрицу
матрицу  называется
называется 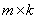 матрица
матрица 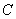 .
. 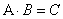 , где
, где 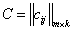
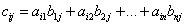 , где
, где 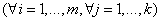
Говорят, что 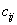 есть скалярное произведение
есть скалярное произведение 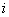 -строки матрицы
-строки матрицы  на
на 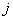 -столбец матрицы
-столбец матрицы  .
.
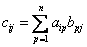 , где
, где 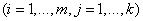
Пример:

Свойства умножения матриц
Умножение матриц ассоциативно:
1) 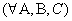
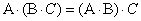 , если определены произведения матриц
, если определены произведения матриц 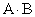 и
и 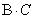
Доказательство:
Пусть 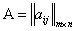 , так как определено
, так как определено 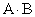 , то
, то 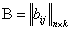 и определено
и определено 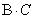 , то
, то 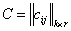
Определим матрицы:
а) 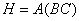
б) 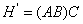
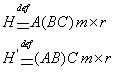 (1) матрицы, тогда
(1) матрицы, тогда  имеют одинаковую размерность
имеют одинаковую размерность
2) Покажем, что на одинаковых местах в матрицах 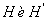 расположены одинаковые элементы
расположены одинаковые элементы
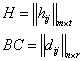 из равенства (1)
из равенства (1) 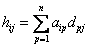 (2),
(2), 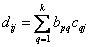 (3). Подставляя (3) в (2) получим:
(3). Подставляя (3) в (2) получим: 
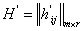
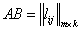 , тогда
, тогда 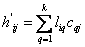 (4),
(4), 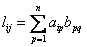 (5). Подставляя (5) в (4) получим:
(5). Подставляя (5) в (4) получим:
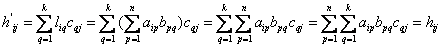
Вывод: Матрицы 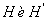 имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.
имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.
Умножение матриц дистрибутивно 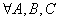 :
: 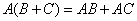
Доказательство:
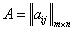 так как определено
так как определено 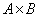 , то
, то 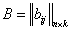 и определено
и определено 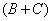 , то
, то 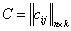
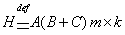 размерности
размерности
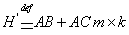 размерности
размерности
Матрицы 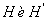 имеют одинаковую размерность, покажем расположение одинаковых элементов:
имеют одинаковую размерность, покажем расположение одинаковых элементов:
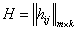 ,
, 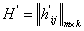
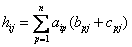 ,
, 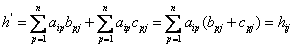
Вывод: На одинаковых местах расположены одинаковые элементы.
3. 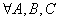 ,
, 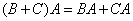 . Если определены
. Если определены 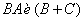 матрицы, то доказательство проводим аналогично свойству 2.
матрицы, то доказательство проводим аналогично свойству 2.
4. 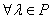 ,
, 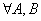 :
: 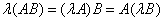 , если определена матрица
, если определена матрица 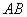
Доказательство:

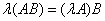 . Пусть
. Пусть 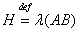 ,
, 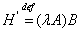
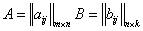 ,
, 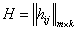 ,
, 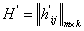
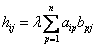
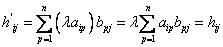
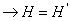
5. Умножение матриц в общем случае не коммутативно. Рассмотрим это на примере:
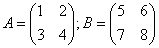 , тогда
, тогда 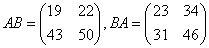
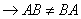
Техника матричного умножения
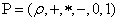 поле скаляров,
поле скаляров, 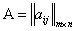 ,
, 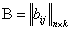
Свойства:
Произведение 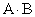 можно рассматривать, как результат умножения столбцов матрицы
можно рассматривать, как результат умножения столбцов матрицы 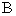 на
на  слева и как результат умножения строк матрицы
слева и как результат умножения строк матрицы  на
на 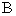 справа.
справа.
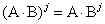
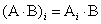
Пусть 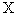 матрица
матрица 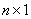 ,
, 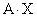 -линейная комбинация столбцов матрицы
-линейная комбинация столбцов матрицы  коэффициенты которой служат элементы матрицы
коэффициенты которой служат элементы матрицы 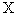
Пример
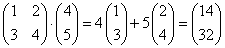
Пусть 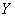 -матрица
-матрица 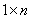 , тогда
, тогда 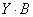 -линейная комбинация строк матрицы
-линейная комбинация строк матрицы 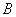 коэффициенты которой служат элементы матрицы
коэффициенты которой служат элементы матрицы 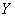
Пример:
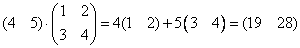
Столбцы матрицы 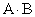 -линейная комбинация столбцов матрицы
-линейная комбинация столбцов матрицы  . Строки
. Строки 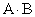 -линейная комбинация строк матрицы
-линейная комбинация строк матрицы 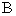 .
.
Транспонирование произведения матриц
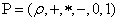 поле скаляров,
поле скаляров, 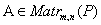 ,
, 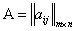 ,
, 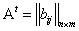 ,
, 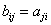
Теорема
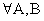 если
если 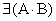 , то
, то 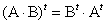 . Обозначим:
. Обозначим: 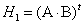 ,
, 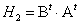
Доказательство:
 1) Пусть
1) Пусть 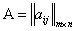 ,
, 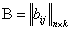
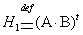 - размерности
- размерности 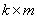 ,
, 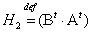 - размерности
- размерности 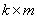 , тогда
, тогда  и
и  имеют одинаковую размерность
имеют одинаковую размерность
2) 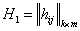 ,
, 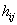 -элемента расположенный в
-элемента расположенный в 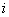 -строке,
-строке, 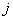 -столбце матрицы
-столбце матрицы 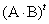 т.е
т.е 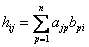
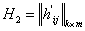 ,
, 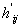 -произведение
-произведение 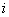 -строки транспонированной
-строки транспонированной 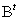 на
на 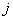 столбец
столбец 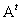 ,
, 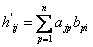
 2015-01-13
2015-01-13 1994
1994
