Введение. При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами

При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.

Цель данной работы: теоретическое обоснование и необходимость практического применения теоремы Коши-Бине:

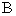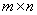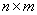Пусть , - и -матрицы соответственно, 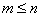и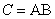

Тогда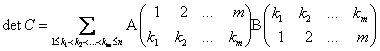

Другими словами, при 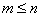определитель матрицы 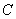является суммой произведений всевозможных миноров порядка 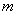в на соответствующие миноры матрицы 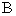того же самого порядка

Работа состоит из четырех глав, содержит заключение, список литературы и приложение программы для теоремы Коши-Бине. В главе 1 рассматриваются элементы линейной алгебры – матрицы, операции над матрицами и свойства сложения матриц, и умножения на скаляр. Глава 2 посвящается умножению матриц и его свойств, а также транспонирование произведения двух матриц. В главе 3 рассматриваются обратимые и элементарные матрицы. В главе 4 вводиться понятие определителя квадратной матрицы, рассматриваются свойства и теоремы об определителях, а также приводится доказательство теоремы Коши-Бине, что является целью моей работы. В дополнение прилагается программа показывающая механизм нахождения определителя произведения двух матриц.