Мы определяем матрицу как прямоугольную таблицу чисел:
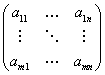
Где элементы матрицы aij (1≤i≤m, 1≤j≤n)-числа из поля 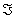 .Для наших целей поле
.Для наших целей поле 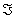 будет либо множеством всех вещественных чисел, либо множеством всех комплексных. Размер матрицы
будет либо множеством всех вещественных чисел, либо множеством всех комплексных. Размер матрицы 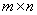 , где m-число строк, n-число столбцов. Если m=n, то говорят, что матрица квадратная, порядка n. В общем случаем матрица называется прямоугольной.
, где m-число строк, n-число столбцов. Если m=n, то говорят, что матрица квадратная, порядка n. В общем случаем матрица называется прямоугольной.
Каждой 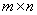 матрице
матрице  с элементами aij соответствует n×m матрица с элементами aji. Она называется транспонированной к
с элементами aij соответствует n×m матрица с элементами aji. Она называется транспонированной к  и обозначается через
и обозначается через 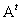 . Видно, что
. Видно, что 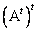 =
=  . Строки матрицы
. Строки матрицы  становятся столбцами в
становятся столбцами в 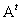 и столбцы матрицы
и столбцы матрицы  становятся строками в
становятся строками в 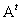 .
.
Матрица называется нулевой если все элементы равны 0:
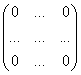
Матрица называется треугольной если все ее элементы, расположенные ниже главной диагонали равны 0

Треугольная матрица называется диагональной, если все элементы расположенные вне главной диагонали равны 0

Диагональной матрица называется единичной, если все элементы расположенные на главной диагонали равны 1
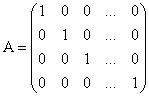
Матрица, составленная из элементов, находящихся на пересечении нескольких выбранных строк матрицы  и нескольких выбранных столбцов, называется субматрицей для матрицы
и нескольких выбранных столбцов, называется субматрицей для матрицы  . Если
. Если 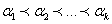 -номера выбранных строк и
-номера выбранных строк и 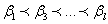 -номера выбранных столбцов, то субматрица это
-номера выбранных столбцов, то субматрица это

В частности, строки и столбцы матрицы можно рассматривать как ее субматрицы.
Определим следующие операции:
Сумма двух 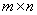 матриц
матриц  , и
, и 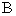 с элементами
с элементами 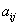 и
и 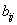 есть
есть 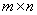 матрица С с элементами
матрица С с элементами 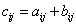 , запишем это как
, запишем это как 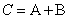
Произведение матрицы  на число
на число 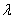 поля
поля 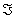 есть матрица С с элементами
есть матрица С с элементами 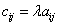 , запишем как
, запишем как 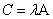 .
.
Произведение 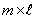 матрицы
матрицы  на
на 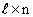 матрицу
матрицу 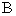 есть
есть 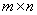 матрица С с элементами
матрица С с элементами 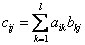 , запишем
, запишем 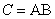
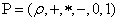 поле скаляров, рассмотрим
поле скаляров, рассмотрим 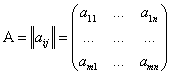 , где
, где 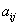 элемент матрицы
элемент матрицы  , расположенный в
, расположенный в 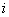 -строке
-строке 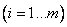 ,
, 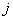 -столбце
-столбце 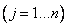 . Размерность матрицы
. Размерность матрицы 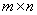 .Если
.Если 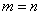 , то
, то  -квадратная матрица порядка
-квадратная матрица порядка 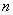 . Множество
. Множество 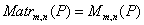 -это множество всех
-это множество всех 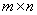 матриц над полем
матриц над полем 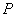 .
.
Опр. Две матрицы равны, если они имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы. Другими словами: 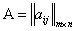 равна матрице
равна матрице 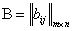 , т.е
, т.е 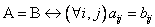
Опр. Пусть 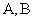 -это матрицы одинаковой размерности
-это матрицы одинаковой размерности 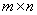 . Суммой матриц
. Суммой матриц  и
и 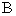 называется
называется 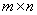 матрица у которой в
матрица у которой в 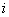 строке,
строке, 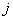 столбце расположен элемент
столбце расположен элемент 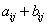 , т.е.
, т.е. 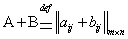 . Другими словами: Чтобы сложить две матрицы нужно сложить соответствующие элементы:
. Другими словами: Чтобы сложить две матрицы нужно сложить соответствующие элементы:
Пример:
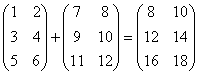
Опр. Пусть 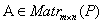 ,
, 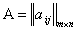 ,
, 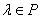 . Произведение скаляра
. Произведение скаляра 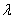 на матрицу
на матрицу  называется
называется 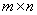 у которой в
у которой в 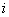 строке,
строке, 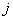 столбце расположен элемент
столбце расположен элемент 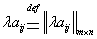 . Другими словами: Чтобы скаляр
. Другими словами: Чтобы скаляр 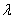 умножить на матрицу
умножить на матрицу  нужно все элементы матрицы
нужно все элементы матрицы  умножить на скаляр
умножить на скаляр 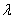 .
.
Определение. Противоположной к матрице  называется матрица
называется матрица 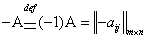
Свойства сложения и умножения матриц на скаляры:
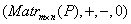 -абелева группа
-абелева группа
1) Сложение матриц 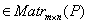 ассоциативно и коммутативно.
ассоциативно и коммутативно.
2) 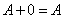
3) 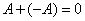
а) 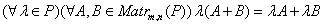
б) 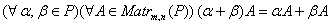
4) 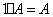
 2015-01-13
2015-01-13 927
927








