2015-01-13
1068
Форма эллипса зависит от отношения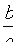 
.При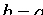 
эллипс превращается в окружность, уравнение эллипса (11.7) принимает вид 
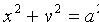. В качестве характеристики формы эллипса чаще пользуются отношением 
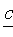. Отношение 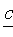половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и o6oзначается буквой ε («эпсилон»):
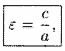(11.8)
причем 0<ε< 1, так как 0<с<а. С учетом равенства (11.6) формулу (11.8) можно переписать в виде
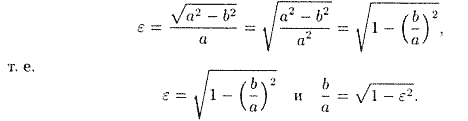
Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить ε = 0, то эллипс превращается в окружность.
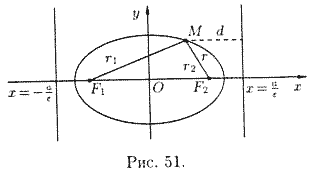Пусть М(х;у) -- произвольная точка эллипса с фокусами F1 и F2 (см. рис. 51). Длины отрезков F1M=r1 и F2M = r2 называются фокальными радиусами точки Μ. Очевидно,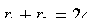 
Имеют место формулы
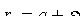и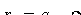 
Прямые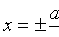 
называются
Теорема 11.1. Если 
— расстояние от произвольной точки эллипса до какого-нибудь фокуса, d — расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение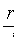 
есть постоянная величина, равная эксцентриситету эллипса: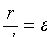 
|
|
|
Из равенства (11.6) следует, что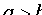 
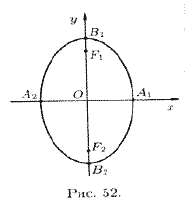
. Если же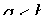 
, то уравнение (11.7) определяет эллипс, большая ось которого 
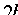лежит на оси Оу, а малая ось 
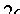— на оси Ох (см. рис. 52). Фокусы такого эллипса находятся в точках 
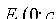и 
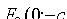, где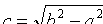 
.
14. Гипербола
