2015-01-13
780
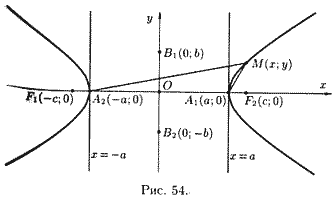
Установим форму гиперболы, пользуясь ее каконическим уравнением.
Уравнение (11.9) содержит x и у только в четных степенях. Следовательно, гипербола симметрична относительно осе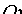й 
и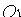 
, а также относительно точки 
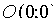, которую называют центром гиперболы.
Найдем точки пересечения гиперболы с осями координат. Положив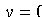 
в уравнении (11.9), находим две точки пересечения гиперболы с осью : 
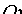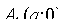и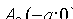 
. Положив 
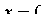в (11.9), получаем 
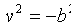, чего быть не может. Следовательно, гипербола ось Оу не пересекает.
Точки 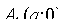и 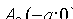называются вершинами гиперболы, а отрезок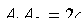 
действительной осью, отрезок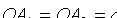 
— действительной полуосью гиперболы.
Отрезок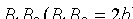 
, соединяющий точки 
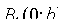и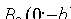 
называется мнимой осью, число b - мнимой полуосью. Прямоугольник со сторонами 2a и 2b называется основным прямоугольником гиперболы.
Из уравнения (11.9) следует, что уменьшаемое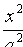 
не меньше единицы т. е. что 
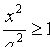или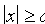 
. Это означает, что точки гиперболы расположены справа от прямой 
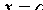(правая ветвь гиперболы) и слева от прямой 
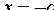(левая ветвь гиперболы).
4. Из уравнения (11.9) гиперболы видно, что когда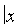 
возрастает, то и 
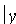возрастает. Это следует из того, что разность 
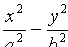сохраняет постоянное значение, равное единице.
Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 54 (кривая, состоящая из двух неограниченных ветвей).
