Метод эквивалентного эллипсоида

Для корпусов малого и сред­него удлинений теория тонкого тела непригодна. Здесь больше под­ходит метод замены исходной конфигурации эквивалентным эллип­соидом. Если исходная конфигурация трехмерна, то и эквивалент­ный эллипсоид следует выбирать трехосным.

Пусть габариты исходного корпуса характеризуются величина­ми: длиной L, шириной В и высотой D. Аналогичные полуоси эллип­соида равны a, b, с и расположены вдоль осей х, у, z соответствен­но. Укажем теперь правила выбора размеров эквивалентного эллип­соида. Предварительно заметим, что помимо указанных габаритов известен также объем 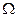исходной конфигурации.

При вычислени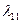и и 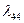следует задавать 2b = B, 2c=D, а тре­тью полуось определять из равенства объемов исходной конфигу­рации и эквивалентного эллипсоида:

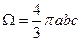
При вычислении 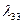, 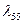нужно задать 2a = L, 2b = B, а третью ось определить на основании равенства объемов.

При вычислении 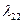, 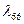нужно задать величины полуосей 2a = L, 2c = D, а третью ось определить из условия равенств объемов.

Полученные присоединенные массы эквивалентного эллипсоида могут считаться приближенно равными присоединенным массам исходного тела.

Если исходная конфигурация представляет собой тело вращения, то в качестве эквивалентного эллипсоида логично использовать так­же эллипсоид вращения.

Пределы применимости теории тонкого тела можно оценить пу­тем сравнения результатов расчетов по этой теории с расчетами по точным формулам для эллипсоидов вращения.

Расширение пределов применимости теории тонкого тела можно осуществить с помощью эмпирических поправок. Для пластин полуразмаха l бесконечного удлинения, как было показано ранее, при­соединенная масса равна

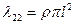
Присоединенная масса прямоугольных пластин конечного удли­нения находится по формуле

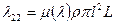(4.49)

где L – длина пластины, 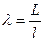- удлинение пластины; 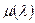– эмпирическая поправка Пабста:

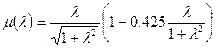(4.50)

Анализ показывает, что та же поправка пригодна и для корректировки расчетов присоединенных масс тел вращения по теории тонкого тела, т. е. можно приближенно считать

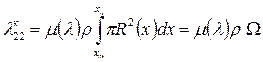(4.51)

и эта формула распространяется уже практически на любые удли­нения.

Расчет 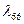для прямоугольных пластин конечного удлинения производится по формуле

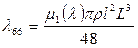(4.52)

где 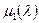– эмпирическая поправка,

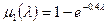(4.53)

Этот же поправочный множитель дает умеренную погрешность в диапазоне 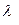~ 4...10 при расчете 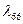эллипсоидов вращения. Сле­довательно, для эллипсоидов вращения можно записать

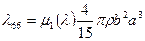. (4.54)

Преимущество формул (4.52), (4.54) в их простоте при достаточной точности результатов.