405
Опр. Поверхность, определяемая в дпск уравнением:
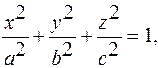(27)
называет эллипсоидом.
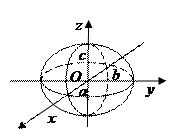
Из уравнения следует, что поверхность симметрична относительно координатных плоскостей, начало координат – её центр симметрии.
Исследуем эту поверхность методом сечений.
1) 
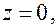
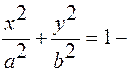это эллипс с осями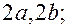 
2) 
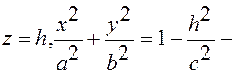это эллипс с полуосями
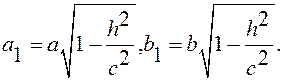
3) Если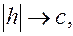 
то полуоси уменьшаются и уменьшаются эллипсы в сечениях;
4) При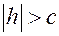 
плоскость 
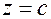поверхность не пересекает.
Аналогично проводится исследование с помощью плоскосте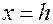й 
и
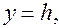параллельных 
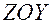и 
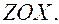
Эллипсоид есть овальная поверхность с тремя плоскостями симметрии;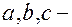 
полуоси эллипсоида. Если 
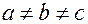, то эллипсоид трехосный. Эллипсоид – ограниченная поверхность, заключенная в параллелепипеде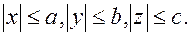 
Если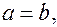 
то в сечениях плоскостями 
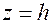получаются окружности.
Этот эллипсоид получается вращением эллипса вокруг оси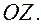 
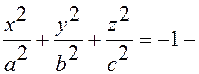мнимый эллипсоид. При 
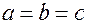имеем сферу.
