2015-01-13
1168
Эксцентриситетом гиперболы (11.9) называется отношение расстояния между фокусами к величине действительной оси гиперболы, обозначается ε:
Так как для гиперболы 
, то эксцентриситет гиперболы больше единицы: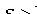 
. Эксцентриситет характеризует форму гиперболы. Действительно, из равенства (11.10) следует, что 
т.е. 
и 
.
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение — ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет равносторонней гиперболы равен 
. Действительно,
Фокальные радиусы 
и 
для точек правой ветви гиперболы имеют вид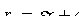 
и 
, а для левой — 
и 
.
Прямые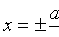 
— называются директрисами гиперболы. Так как для гиперболы ε > 1, то 
. Это значит, что правая директриса расположена между центром и правой вершиной гиперболы, левая — между центром и левой вершиной.
Директрисы гиперболы имеют то же свойство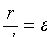 
, что и директрисы эллипса.
Кривая, определяемая уравнением 
также есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2 a — на оси Ох. На рисунке 59 она изображена пунктиром.
|
|
|
Очевидно, что гиперболы 
и имеют общие асимптоты. Такие гиперболы называются сопряженными.
