Эллипсоид

Исследуем поверхность, заданную уравнением:

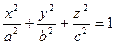
Рассмотрим сечения поверхности с плоскостями, параллельными плоскости xOy. Уравнения таких плоскостей: z=h,гдеh – любое число. Линия, получаемая в сечении, определяется двумя ур-ниями:

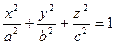
z=h.

Исследуем поверхность:

А) если 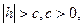то 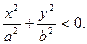Линия пересечения поверхности с плоскостямиz=h не существует.

Б) если 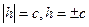, 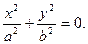линия пересечения вырождается в две точки (0,0,с), и (0,0,-с). Плоскости z = c, z = - c касается данной поверхности.

В) если 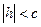, то уравнения можно переписать в виде: 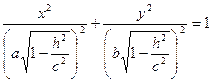, как видно, линия пересечения есть эллипс с полуосями а1 = 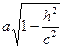, b1 = 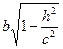. При этом, чем меньше h, тем больше полуоси. При н=0 они достигают своих наибольших значений. а1=а, b1=b. Уравнения примут вид:

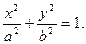
h=0.

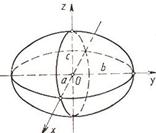
Рассмотренные сечения позволяют изобразить поверхность как замкнутую овальную поверхность. Поверхность называется эллипсоидами., если какие-либо полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения, а если а=b=c, то в сферу.