Экстремум ф-ции нескольких переменных. Теорема(необходимые условия экстремума): Если в точке N(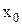 , , 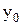 ) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю: ) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю: 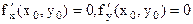 . Док-во: Зафиксируем одну из переменных. Положим, y= . Док-во: Зафиксируем одну из переменных. Положим, y= 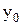 . Тогда получим ф-цию . Тогда получим ф-цию 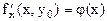 одной переменной, которая имеет экстремум при x- одной переменной, которая имеет экстремум при x- 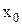 . Следовательно, согласно необходимому условию экстремума функции одной переменной, . Следовательно, согласно необходимому условию экстремума функции одной переменной, 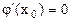 , т.е. , т.е. 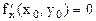 . Замеч.: ф-ция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Точка, в которой частные производные первого порядка функции z=f(x,y) равны нулю, т.е. . Замеч.: ф-ция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Точка, в которой частные производные первого порядка функции z=f(x,y) равны нулю, т.е. 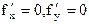 , называется стационарной точкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Теорема(достаточное условие экстремума): Пусть в стационарной точке , называется стационарной точкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Теорема(достаточное условие экстремума): Пусть в стационарной точке 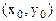 и некоторой ее окрестности функция F(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке и некоторой ее окрестности функция F(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 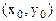 значения значения 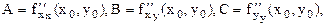 обозначим обозначим 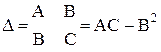 . Тогда: 1.Если . Тогда: 1.Если 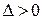 , то функция f(x,y) в точке , то функция f(x,y) в точке 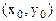 имеет экстремум: максимум, если A<0, минимум, если A>0; 2.Если имеет экстремум: максимум, если A<0, минимум, если A>0; 2.Если 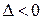 , то функция f(x,y) в точке , то функция f(x,y) в точке 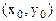 экстремума не имеет. В случае экстремума не имеет. В случае 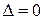 экстремум в точке экстремум в точке 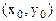 может быть, может не быть. Необходимы дополнительные исследования. 42. Условный экстремум. Метод множителей Лагранжа. Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции z = f (x, y) в точке M 0(x 0; y 0) называется экстремум этой функции, достигнутый при условии, что переменные x и y в окрестности данной точки удовлетворяют уравнению связи φ (x, y)=0. Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие φ (x, y)=0. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует y = ψ (x), то подставив y = ψ (x) в z = f (x, y), получим функцию одной переменной z = f (x, ψ (x)). В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма. Метод множителей Лагранжа для функций двух переменных. Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: F (x, y)= f (x, y)+ λφ (x, y) (параметр λ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки: может быть, может не быть. Необходимы дополнительные исследования. 42. Условный экстремум. Метод множителей Лагранжа. Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции z = f (x, y) в точке M 0(x 0; y 0) называется экстремум этой функции, достигнутый при условии, что переменные x и y в окрестности данной точки удовлетворяют уравнению связи φ (x, y)=0. Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие φ (x, y)=0. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует y = ψ (x), то подставив y = ψ (x) в z = f (x, y), получим функцию одной переменной z = f (x, ψ (x)). В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма. Метод множителей Лагранжа для функций двух переменных. Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: F (x, y)= f (x, y)+ λφ (x, y) (параметр λ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки: 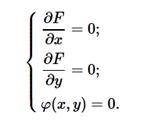 Достаточным условием, из которого можно выяснить характер экстремума, служит знак d 2 F = F ′′ xxdx 2+2 F ′′ xydxdy + F ′′ yydy 2. Если в стационарной точке d 2 F >0, то функция z = f (x, y) имеет в данной точке условный минимум, если же d 2 F <0, то условный максимум. Примечание (желательное для более полного понимания текста): показать\скрыть Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: φ ′ xdx + φ ′ ydy =0, dy =− φ ′ xφ ′ ydx, поэтому в любой стационарной точке имеем: d 2 F = F ′′ xxdx 2+2 F ′′ xydxdy + F ′′ yydy 2= F ′′ xxdx 2+2 F ′′ xydx (− φ ′ xφ ′ ydx)+ F ′′ yy (− φ ′ xφ ′ ydx)2==− dx 2(φ ′ y)2⋅(−(φ ′ y)2 F ′′ xx +2 φ ′ xφ ′ yF ′′ xy −(φ ′ x)2 F ′′ yy) Второй сомножитель (расположенный в скобке) можно представить в такой форме: Достаточным условием, из которого можно выяснить характер экстремума, служит знак d 2 F = F ′′ xxdx 2+2 F ′′ xydxdy + F ′′ yydy 2. Если в стационарной точке d 2 F >0, то функция z = f (x, y) имеет в данной точке условный минимум, если же d 2 F <0, то условный максимум. Примечание (желательное для более полного понимания текста): показать\скрыть Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: φ ′ xdx + φ ′ ydy =0, dy =− φ ′ xφ ′ ydx, поэтому в любой стационарной точке имеем: d 2 F = F ′′ xxdx 2+2 F ′′ xydxdy + F ′′ yydy 2= F ′′ xxdx 2+2 F ′′ xydx (− φ ′ xφ ′ ydx)+ F ′′ yy (− φ ′ xφ ′ ydx)2==− dx 2(φ ′ y)2⋅(−(φ ′ y)2 F ′′ xx +2 φ ′ xφ ′ yF ′′ xy −(φ ′ x)2 F ′′ yy) Второй сомножитель (расположенный в скобке) можно представить в такой форме:  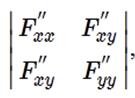 Красным цветом выделены элементы определителя который является гессианом функции Лагранжа. Если H >0, то d 2 F <0, что указывает на условный максимум. Аналогично, при H <0 имеем d 2 F >0, т.е. имеем условный минимум функции z = f (x, y). Примечание относительно формы записи определителя H:показать\скрыть Алгоритм исследования функции двух переменных на условный экстремум Красным цветом выделены элементы определителя который является гессианом функции Лагранжа. Если H >0, то d 2 F <0, что указывает на условный максимум. Аналогично, при H <0 имеем d 2 F >0, т.е. имеем условный минимум функции z = f (x, y). Примечание относительно формы записи определителя H:показать\скрыть Алгоритм исследования функции двух переменных на условный экстремум 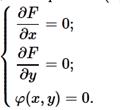 Составить функцию Лагранжа F (x, y)= f (x, y)+ λφ (x, y) 2. Решить систему 3.Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов: Составить определитель H и выяснить его знак С учетом уравнения связи вычислить знак d 2 F Метод множителей Лагранжа для функций n переменных Допустим, мы имеем функцию n переменных z = f (x 1, x 2,…, xn) и m уравнений связи (n > m): φ 1(x 1, x 2,…, xn)=0; φ 2(x 1, x 2,…, xn)=0,…, φm (x 1, x 2,…, xn)=0. Обозначив множители Лагранжа как λ 1, λ 2,…, λm, составим функцию Лагранжа: F (x 1, x 2,…, xn, λ 1, λ 2,…, λm)= f + λ 1 φ 1+ λ 2 φ 2+…+ λmφm Составить функцию Лагранжа F (x, y)= f (x, y)+ λφ (x, y) 2. Решить систему 3.Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов: Составить определитель H и выяснить его знак С учетом уравнения связи вычислить знак d 2 F Метод множителей Лагранжа для функций n переменных Допустим, мы имеем функцию n переменных z = f (x 1, x 2,…, xn) и m уравнений связи (n > m): φ 1(x 1, x 2,…, xn)=0; φ 2(x 1, x 2,…, xn)=0,…, φm (x 1, x 2,…, xn)=0. Обозначив множители Лагранжа как λ 1, λ 2,…, λm, составим функцию Лагранжа: F (x 1, x 2,…, xn, λ 1, λ 2,…, λm)= f + λ 1 φ 1+ λ 2 φ 2+…+ λmφm
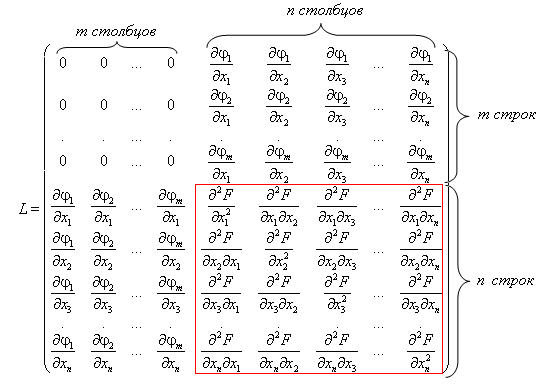
Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа: Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака d 2 F. Если в найденной точке d 2 F >0, то функция имеет условный минимум, если же d 2 F <0, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:
Определитель матрицы, выделенной в матрице L красным цветом, есть гессиан функции Лагранжа. Найдя в каждой стационарной точке значение определителя H =Δ L, используем следующее правило: Если знаки угловых миноров H 2 m +1, H 2 m +2,…, Hm + n матрицы L совпадают с знаком (−1) m, то исследуемая стационарная точка является точкой условного минимума функции z = f (x 1, x 2, x 3,…, xn). Если знаки угловых миноров H 2 m +1, H 2 m +2,…, Hm + n чередуются, причём знак минора H 2 m +1 совпадает с знаком числа (−1) m +1, то исследуемая стационарная точка является точкой условного максимума функции z = f (x 1, x 2, x 3,…, xn). Пример №1 Найти условный экстремум функции z (x, y)= x +3 y при условии x 2+ y 2=10. Решение Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости z = x +3 y для точек ее пересечения с цилиндром x 2+ y 2=10. Выразить одну переменную через другую из уравнения связи и подставить ее в функцию z (x, y)= x +3 y несколько затруднительно, поэтому будем использовать метод Лагранжа. Обозначив φ (x, y)= x 2+ y 2−10, составим функцию Лагранжа: F (x, y)= z (x, y)+ λφ (x, y)= x +3 y + λ (x 2+ y 2−10);∂ F ∂ x =1+2 λx;∂ F ∂ y =3+2 λy.
Запишем систему уравнений для определения стационарных точек функции Лагранжа: Если предположить λ =0, то первое уравнение станет таким: 1=0. Полученное противоречие говорит о том, что λ ≠0. При условии λ ≠0 из первого и второго уравнений имеем: x =−12 λ, y =−32 λ. Подставляя полученные значения в третье уравнение, получим:
d 2 F = F ′′ xxdx 2+2 F ′′ xydxdy + F ′′ yydy 2=2 λ (dx 2+ dy 2) Отмечу, что запись dx 2 означает именно dx, возведённый в вторую степень, т.е. (dx)2. Отсюда имеем: dx 2+ dy 2>0, посему при λ 1=−12 получим d 2 F <0. Следовательно, функция имеет в точке M 1(1;3) условный максимум. Аналогично, в точке M 2(−1;−3) получим условный минимум функции z (x, y)= x +3 y. Отметим, что для определения знака d 2 F не пришлось учитывать связь между dx и dy, ибо знак d 2 F очевиден без дополнительных преобразований. В следующем примере для определения знака d 2 F уже будет необходимо учесть связь между dx и dy. Пример №2 Найти условный экстремум функции z (x, y)=3 y 3+4 x 2− xy при условии x + y =0. Решение |
Экстремумы функций нескольких переменных
|
|
Подборка статей по вашей теме:
- Представление логической функции в виде СДНФ и СКНФ
- Функция strncat
- Типы в функциональных языках
- Найдем значение функции f2 на противоположных наборах аргументов
- П.5. Обратная функция
- Передаточные и переходные функции типовых динамических звеньев
- Дифференцируемость и полный дифференциал функции
- Понятие и функция расходов на производство
- Лекция № 23 Предел и непрерывность функции нескольких переменных
- Функции, проблемы
- Функции, определяемые пользователем
- Вызов функции
 2015-01-13
2015-01-13 2297
2297

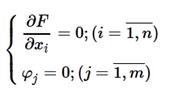
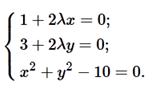
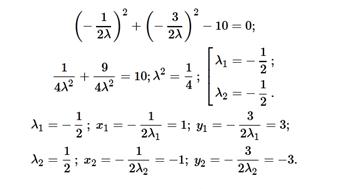 Итак, система имеет два решения: x 1=1; y 1=3; λ 1=−12 и x 2=−1; y 2=−3; λ 2=12. Выясним характер экстремума в каждой стационарной точке: M 1(1;3) и M 2(−1;−3). Для этого вычислим определитель H в каждой из точек.
Итак, система имеет два решения: x 1=1; y 1=3; λ 1=−12 и x 2=−1; y 2=−3; λ 2=12. Выясним характер экстремума в каждой стационарной точке: M 1(1;3) и M 2(−1;−3). Для этого вычислим определитель H в каждой из точек. Вопрос о характере экстремума в стационарных точках M 1(1;3) и M 2(−1;−3) можно решить и без использования определителя H. Найдем знак d 2 F в каждой стационарной точке:
Вопрос о характере экстремума в стационарных точках M 1(1;3) и M 2(−1;−3) можно решить и без использования определителя H. Найдем знак d 2 F в каждой стационарной точке: