Пусть функция z=f(x,y) дифференцируема в точке 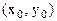 некоторой области
некоторой области 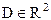 . Рассечем поверхность S, изображающую функцию z, плоскостями x=
. Рассечем поверхность S, изображающую функцию z, плоскостями x= 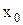 и y=
и y= 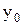 . Плоскость x=
. Плоскость x= 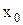 пересекает поверхность S по некоторой линии
пересекает поверхность S по некоторой линии 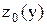 , уравнение которой получается подстановкой в выражение исходной функции z=f(x,y) вместо х числа
, уравнение которой получается подстановкой в выражение исходной функции z=f(x,y) вместо х числа 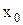 . Точка
. Точка 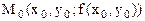 принадлежит кривой
принадлежит кривой 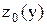 . В силу дифференцируемости функции z в точке
. В силу дифференцируемости функции z в точке 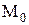 функция
функция 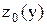 также является дифференцируемой в точке y=
также является дифференцируемой в точке y= 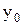 . Следовательно, в этой точке в плоскости x=
. Следовательно, в этой точке в плоскости x= 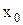 к кривой
к кривой 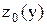 может быть проведена касательная
может быть проведена касательная 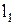 . Построим касательную
. Построим касательную 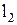 к кривой
к кривой 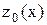 в точке x=
в точке x= 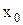 . Прямые
. Прямые 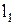 и
и 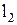 определяют плоскость
определяют плоскость 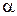 , которая называется касательной плоскостью к поверхности S в точке
, которая называется касательной плоскостью к поверхности S в точке 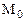 . Составим ее уравнение. Так как плоскость
. Составим ее уравнение. Так как плоскость 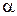 проходит через точку
проходит через точку 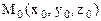 , то ее уравнение может быть записано в виде А(
, то ее уравнение может быть записано в виде А(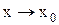 ) + В(
) + В(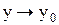 ) + С(
) + С( )=0, которое можно переписать так:
)=0, которое можно переписать так: 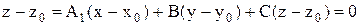 (разделив уравнение на –С и обозначив А/-С=
(разделив уравнение на –С и обозначив А/-С= 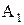 , В/-С=
, В/-С=  ). Найдем
). Найдем 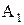 и
и  . Уравнения касательных имеют вид:
. Уравнения касательных имеют вид: 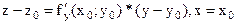 ;
;  соответственно. Касательная
соответственно. Касательная 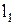 лежит в плоскости
лежит в плоскости 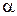 .
. 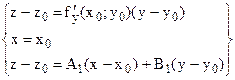 . В итоге
. В итоге 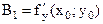 . Следовательно,
. Следовательно,  . Искомое уравнение касательной плоскости:
. Искомое уравнение касательной плоскости: 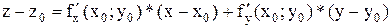 . Прямая, проходящая через точку
. Прямая, проходящая через точку 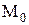 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью. Каноническое уравнение нормали:
и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью. Каноническое уравнение нормали: 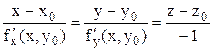 .
.
Касательная плоскость и нормаль к поверхности
|
|

Сейчас читают про:
 2015-01-13
2015-01-13 563
563







