Второй способ

Из уравнения связи x + y =0 получим: y =− x. Подставив y =− x в функцию z (x, y)=3 y 3+4 x 2− xy, имеем:

z =3⋅(− x)3+4 x 2− x ⋅(− x)=−3 x 3+5 x 2.

Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.

z ′ x =−9 x 2+10 x;−9 x 2+10 x =0; x ⋅(−9 x +10)=0; x 1=0; y 1=− x 1=0; x 2=109; y 2=− x 2=−109.

Получили точки M 1(0;0) и M 2(109;−109). Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак z ′′ xx в каждой стационарной точке или проверяя смену знака z ′ x в найденных точках, получим те же выводы, что и при решении первым способом.

Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака d 2 F.

Пример №3

Найти наибольшее и наименьшее значения функции z =5 xy −4, если переменные x и y положительны и удовлетворяют уравнению связи x 28+ y 22−1=0.

Решение

Составим функцию Лагранжа: F =5 xy −4+ λ (x 28+ y 22−1). Найдем стационарные точкифункции Лагранж а:

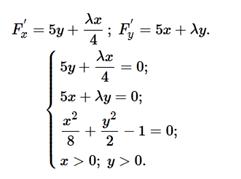Все дальнейшие преобразования осуществляются с учетом x >0; y >0 (это оговорено в условии задачи). Из второго уравнения выразим λ =−5 xy и подставим найденное значение в первое уравнение: 5 y −5 xy ⋅ x 4=0, 4 y 2− x 2=0, x =2 y. Подставляя x =2 y в третье уравнение, получим: 4 y 28+ y 22−1=0, y 2=1, y =1.

Так как y =1, то x =2, λ =−10. Характер экстремума в точке (2;1) определим, исходя из знака d 2 F.

F ′′ xx = λ 4; F ′′ xy =5; F ′′ yy = λ.

Так как x 28+ y 22−1=0, то:

d (x 28+ y 22−1)=0; d (x 28)+ d (y 22)=0; x 4 dx + ydy =0; dy =− xdx 4 y.

В принципе, здесь можно сразу подставить координаты стационарной точки x =2, y =1 и параметра λ =−10, получив при этом:

F ′′ xx =−52; F ′′ xy =−10; dy =− dx 2. d 2 F = F ′′ xxdx 2+2 F ′′ xydxdy + F ′′ yydy 2=−52 dx 2+10 dx ⋅(− dx 2)−10⋅(− dx 2)2==−52 dx 2−5 dx 2−52 dx 2=−10 dx 2.

Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше d 2 F представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

d 2 F = F ′′ xxdx 2+2 F ′′ xydxdy + F ′′ yydy 2= λ 4 dx 2+10⋅ dx ⋅− xdx 4 y + λ ⋅(− xdx 4 y)2== λ 4 dx 2−5 x 2 ydx 2+ λ ⋅ x 2 dx 216 y 2=(λ 4−5 x 2 y + λ ⋅ x 216 y 2)⋅ dx 2