Пусть z = f (x; у) - функция двух переменных х и у, каждая из которых является функцией независимой переменной t: х = x(t), у = y(t). В этом случае функция z = f(x(t); y(t)) является сложной функцией одной независимой переменной t; переменные х и у - промежуточные переменные.
Теорема 44.4.
Если z = f (x; у) - дифференцируемая в точке М (х; у) ∈ D функция и х = x(t) и
у = y(t) – дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = f(x(t); y(t)) вычисляется по формуле
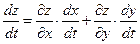 (44.8)
(44.8)
Частный случай: z = f (x; у), где у = у(х), т. е. z = f (x; у(х)) - сложная функция одной независимой переменной х. Этот случай сводится к предыдущему, причем роль переменной t играет х.Согласно формуле (44.8) имеем:
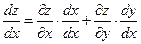 или
или 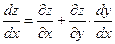 (44.9)
(44.9)
Формула (44.9) носит название формулы полной. Производной.
Общий. случай: z = f (x; у), где х = х (u; v), у = у (u; v). Тогда
z = f (x (u; v); у(u; v)) - сложная функция независимых переменных u и v. Ее частные производные 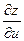 и
и 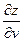 можно найти, используя формулу (44.8) следующим образом. Зафиксировав v, заменяем в ней
можно найти, используя формулу (44.8) следующим образом. Зафиксировав v, заменяем в ней 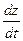 ,
, 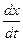 ,
, 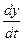 соответствующими частными производными
соответствующими частными производными 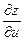 ,
, 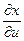 ,
, 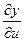 :
:
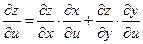 (44.10)
(44.10)
Аналогично получаем: 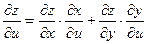
 2015-01-13
2015-01-13 683
683








