
þ 3/5

þ 3/2
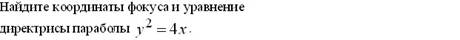
þ (1; 0); Х= -1

þ 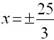
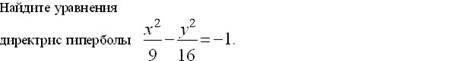
þ 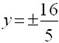
Уравнение гиперболы с полуосями а=3,в=5,
действительной осью ОХ и центром в начале
координат имеет вид:
þ 
Установите соответствие:
| окружность | 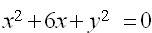 |
| эллипс |  |
| гипербола | 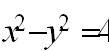 |
| парабола | 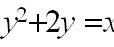 |
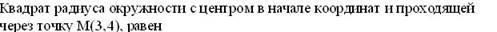
Эталон(ы) ответа: 25
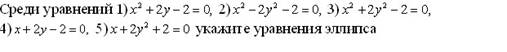
Эталон(ы) ответа: 3
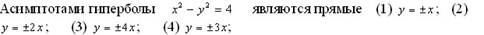
Эталон(ы) ответа: 1

Эталон(ы) ответа: 13
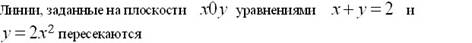
þ только в 1 и 2 четверти
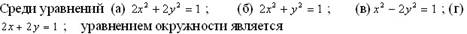
þ а
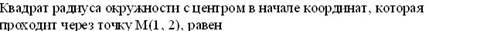
Эталон(ы) ответа: 5
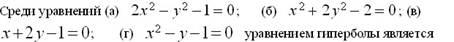
þ а
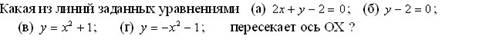
þ а
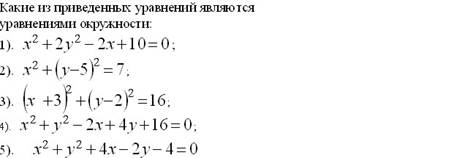
þ 
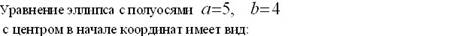
þ 
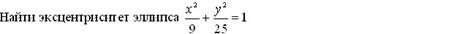
þ 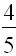
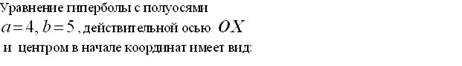
þ 

þ 
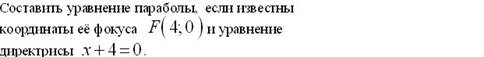
þ 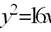

þ 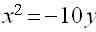
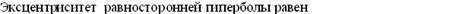
þ 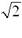
Определить пары параллельных прямых
| 3x+6y+2=0 | y=-0,5x+2 |
| 4x-2y+5=0 | y=2x-3 |
| 6x-2y-7=0 | y=3x-5 |
Определить пары перпендикулярных прямых
| y=-0,5x+2 | -2x+y-13=0 |
| y=2x-3 | 0,5x+y-7=0 |
| y=3x-5 | -2x-6y+5=0 |
Определить пары параллельных прямых
| 12x-3y+7=0 | y=4x-5 |
| 14x-7y-3=0 | y=2x+2 |
| 10x+2y-1=0 | y=-5x+1 |
Определить пары перпендикулярных прямых
| 2x+8y-5=0 | y=4x-5 |
| x+2y+3=0 | y=2x+2 |
| -2x-10y+7=0 | y=5x+1 |
Определить пары параллельных прямых
| 6x+8y-1=0 | y=-0,75x |
| 10x-4y+3=0 | y=2,5x-3 |
| 9x-5y+3=0 | y=1,8x+2 |
Определить пары перпендикулярных прямых
| 8x-6y+5=0 | y=-0,75x |
| -4x-10y+3=0 | y=2,5x-3 |
| 5x+8y-3=0 | y=1,6x+2 |
Определить пары параллельных прямых
| 6x-2y-7=0 | y=3x-5 |
| 3x+6y+2=0 | y=-0,5x+2 |
| 4x-2y+5=0 | y=2x-3 |
Определить пары перпендикулярных прямых
| y=-0,5x+2 | -2x+y-13=0 |
| y=2x-3 | 0,5x+y-7=0 |
| y=3x-5 | -2x-6y+5=0 |
Определить пары параллельных прямых
| 12x-3y+7=0 | y=4x-5 |
| 14x-7y-3=0 | y=2x+2 |
| 10x+2y-1=0 | y=-5x+1 |
Определить пары перпендикулярных прямых
| 2x+8y-5=0 | y=4x-5 |
| x+2y+3=0 | y=2x+2 |
| -2x-10y+7=0 | y=5x+1 |
Определить пары параллельных прямых
| 6x+8y-1=0 | y=-0,75x |
| 10x-4y+3=0 | y=2,5x-3 |
| 9x-5y+3=0 | y=1,8x+2 |
Определить пары перпендикулярных прямых
| 8x-6y+5=0 | y=-0,75x |
| -4x-10y+3=0 | y=2,5x-3 |
| 5x+8y-3=0 | y=1,6x+2 |
Определить пары параллельных прямых
| 3x+6y+2=0 | y=-0,5x+2 |
| 4x-2y+5=0 | y=2x-3 |
| 6x-2y-7=0 | y=3x-5 |
Определить пары перпендикулярных прямых
| y=-0,5x+2 | -2x+y-13=0 |
| y=2x-3 | 0,5x+y-7=0 |
| y=3x-5 | -2x-6y+5=0 |
Определить пары параллельных прямых
| 12x-3y+7=0 | y=4x-5 |
| 14x-7y-3=0 | y=2x+2 |
| 10x+2y-1=0 | y=-5x+1 |
Укажите угловой коэффициент прямой
2x+5y-1=0
þ -2/5
Укажите координаты нормального
вектора прямой 4x - 3y + 7 = 0
þ (4; -3)
Найдите отрезок, отсекаемый прямой
5x + 2y - 4 = 0 на оси ординат
þ 2
Найдите расстояние от точки Р (3; 1) до
прямой 2x + y + 3 = 0
þ 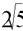

þ 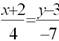
Уравнение прямой, проходящей через
точки А (1; 2) и В (-2; 3), имеет вид:
þ x + 3y - 7 = 0
Общим уравнением прямой на
плоскости является:
þ 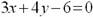
Какие из следующих прямых перпендикулярны:
1. 2x-3y+4=0
2. 2x+3y+4=0
3. x-3y+8=0
4. 3x+2y-4=0
þ 1 и 4
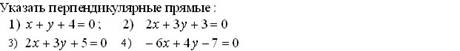
þ 
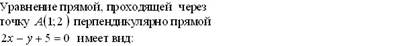
þ 

þ 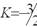

þ 
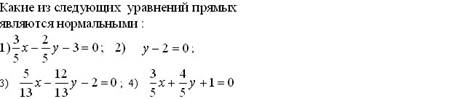
þ 
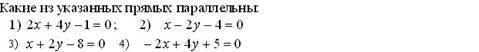
þ 
Укажите все плоскости, которые перпендикулярны вектору (1,1,0)
þ 2x+2y-3=0
þ 3x+3y-8=0
Укажите все плоскости, которые параллельны плоскости 2x+y-z-3=0
þ 4x+2y-2z+2=0
Укажите все плоскости, которые перпендикулярны вектору (1; 0,5; -0,5)
þ 2x+y-z-1=0
þ 4x+2y-2z+3=0
Укажите все плоскости, которые параллельны плоскости 3x+6y+2z-3=0
þ 1.5x+3y+z-4=0
Укажите все плоскости, которые перпендикулярны вектору (1; -1; -2)
þ -x+y+2z+3=0
Укажите все плоскости, которые перпендикулярны вектору (1,1,0)
þ 2x+2y-3=0
þ 3x+3y-8=0
Укажите все плоскости, которые параллельны плоскости 2x+y-z-3=0
þ 4x+2y-2z+2=0
Укажите все плоскости, которые перпендикулярны вектору (1; 0,5; -0,5)
þ 2x+y-z-1=0
þ 4x+2y-2z+3=0
Укажите все плоскости, которые параллельны плоскости 3x+6y+2z-3=0
þ 1.5x+3y+z-4=0
Укажите все плоскости, которые перпендикулярны вектору (1; -1; -2)
þ -x+y+2z+3=0
Укажите все плоскости, которые перпендикулярны вектору (1,1,0)
þ 2x+2y-3=0
þ 3x+3y-8=0
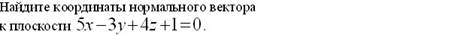
þ (5; -3; 4)
Установите соответствие:
| общее уравнение плоскости |  |
| уравнение плоскости в отрезках | 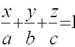 |
| уравнение плоскости через заданную точку | 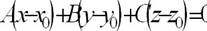 |
| уравнение плоскости, проходящей через начало координат | 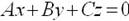 |
| уравнение плоскости, параллельной оси ОХ | 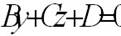 |
| уравнение плоскости, параллельной ХОУ | 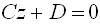 |
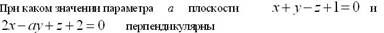
Эталон(ы) ответа: 1
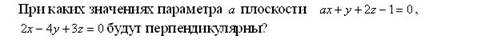
Эталон(ы) ответа: -1
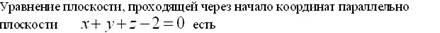
þ 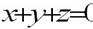
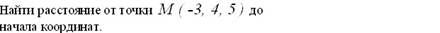
þ 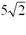
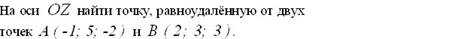
þ 

þ 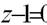
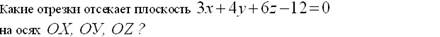
þ 

þ 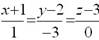
Условие параллельности двух
прямых через угловые коэффициенты
þ 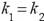
Укажите условия перпендикулярности двух
прямых через координаты нормальных векторов.
þ 
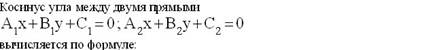
þ 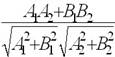
Уравнение прямой через две точки имеет вид
þ 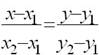
Тангенс угла между прямыми вычисляется по формуле:
þ 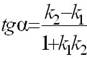
Прямая на плоскости задается:
þ уравнением первой степени относительно текущих координат (x, y)
Установите соответствие
| прямая в отрезках | 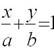 |
| каноническое уравнение прямой | 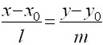 |
| параметрическое уравнение прямой | 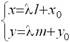 |
| общее уравнение прямой | 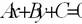 |
| уравнение прямой с угловым коэффициентом | 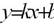 |
| нормальное уравнение прямой | 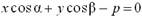 |
Указать соответствие для двух прямых
A1x+B1y+C1=0 и A2x+B2y+C2=0
| пересекаются | 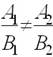 |
| параллельны | 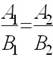 |
| совпадают | 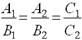 |
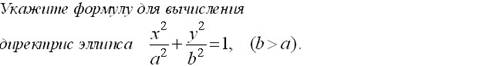
þ 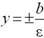

þ 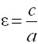
Укажите свойство директрисс для
эллипса и гиперболы:
þ 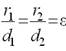
Установить соответствие кривых их эксцентриситету:
| окружность | 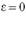 |
| эллипс | 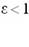 |
| гипербола | 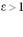 |
| парабола | 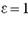 |
Укажите соответствие формул для вычисления фокального расстояния:
 | 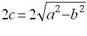 |
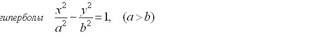 | 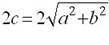 |
 | 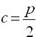 |
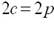 |
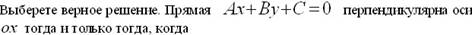
þ 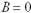
Введите пропущенное слово

Эталон(ы) ответа: эллипс, эллипсом, элипс, элипсом

Эталон(ы) ответа: гипербола, гиперболой
 Эталон(ы) ответа: параболой, парабола
Эталон(ы) ответа: параболой, парабола
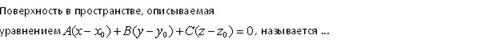
Эталон(ы) ответа: плоскостью, плоскость

Эталон(ы) ответа: плоскость, плоскостью

Эталон(ы) ответа: плоскость, плоскостью
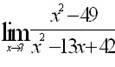
Эталон(ы) ответа: 14
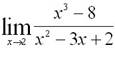
Эталон(ы) ответа: 12
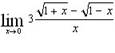
Эталон(ы) ответа: 3
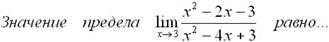
Эталон(ы) ответа: 2
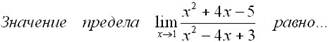
Эталон(ы) ответа: -3
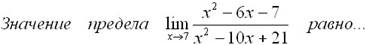
Эталон(ы) ответа: 2
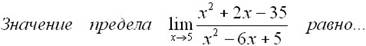
Эталон(ы) ответа: 3
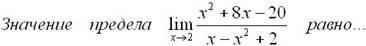
Эталон(ы) ответа: -4
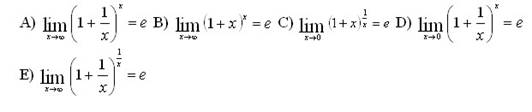
þ 
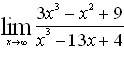
Эталон(ы) ответа: 3
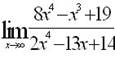
Эталон(ы) ответа: 4
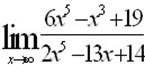
Эталон(ы) ответа: 3
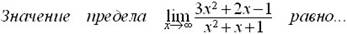
þ 
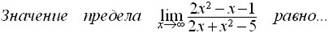
þ 
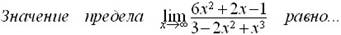
þ 
þ 
þ 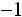
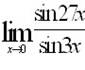
Эталон(ы) ответа: 9
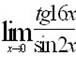
Эталон(ы) ответа: 8
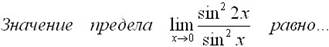
þ 
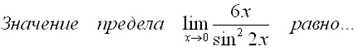
þ 
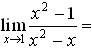
Эталон(ы) ответа: 2
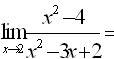
Эталон(ы) ответа: 4
 2015-01-13
2015-01-13 1304
1304








