Сложение. Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц 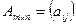 и
и 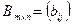 называется матрица
называется матрица 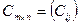 такая, что
такая, что 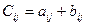
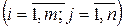 .
.
Пример. 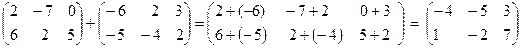
Аналогично определяется разность матриц.
Умножение на число. Произведением матрицы 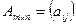 на число
на число 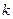 называется матрица
называется матрица 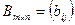 такая, что
такая, что 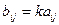
Пример. Найти произведение матрицы 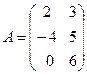 на число
на число 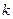 = 2.
= 2.
Решение.
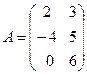 ,
, 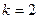 , k A =
, k A = 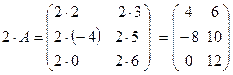
Произведение матриц. Операция умножения двух матриц А и В вводится только для случая, когда число столбцов первой матрицы А равно числу строк второй матрицы В.
Произведением матрицы 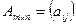 на матрицу
на матрицу 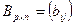 называется матрица
называется матрица 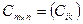 такая, что
такая, что 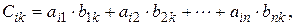 где
где 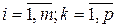 .
.
Получение элемента 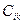 схематично изображается так:
схематично изображается так:
 |
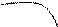
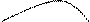
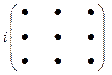
k
Пример. Найти произведение матриц А и В (если это возможно)
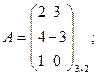
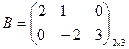 .
.
Решение.
Произведение матриц А и В существует, так как число столбцов матрицы А совпадает с числом строк матрицы В.
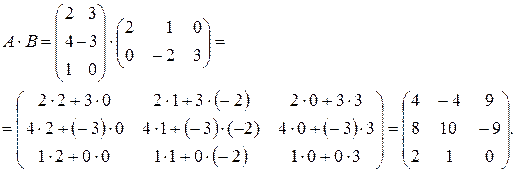
 2015-01-21
2015-01-21 820
820








