6.1. Метод Жордана-Гаусса решения систем линейных уравнений
Пусть дана система линейных уравнений:

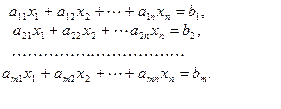 (1)
(1)
В матрице А выберем отличный от нулю элемент 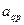 . Этот элемент называется разрешающим элементом, p-ый столбец матрицы А – разрешающим столбцом, а q-ая строка – разрешающей.
. Этот элемент называется разрешающим элементом, p-ый столбец матрицы А – разрешающим столбцом, а q-ая строка – разрешающей.
Рассмотрим новую систему уравнений:
 |
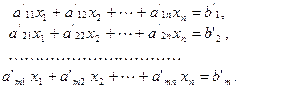 (2)
(2)
с матрицей 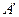 ; коэффициенты и свободные члены этой системы определяются по формулам
; коэффициенты и свободные члены этой системы определяются по формулам
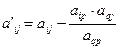
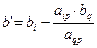 если
если 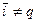 .
.
В частности 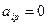 , если
, если 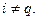 Если же
Если же 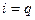 , то принимаем
, то принимаем 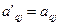 ,
, 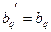 . Таким образом q-е уравнение в системах (1) и (2) одинаково, а коэффициенты при
. Таким образом q-е уравнение в системах (1) и (2) одинаково, а коэффициенты при 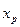 во всех уравнениях системы (2), кроме q-го, равны нулю.
во всех уравнениях системы (2), кроме q-го, равны нулю.
Следует иметь в виду, что системы (1) и (2) одновременно совместны или несовместны. В случае совместности эти системы равносильны (их решения совпадают).
Для определения элемента 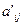 матрицы
матрицы 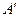 полезно иметь в виду так называемое “правило прямоугольника”.
полезно иметь в виду так называемое “правило прямоугольника”.
Рассмотрим 4 элемента матрицы А: 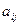 (элемент, подлежащий преобразованию)
(элемент, подлежащий преобразованию) 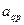 (разрешающий элемент) и элементы
(разрешающий элемент) и элементы 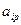 и
и 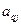 . Для нахождения элемента
. Для нахождения элемента 

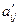
 следует из элемента
следует из элемента 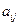 вычесть произведение элементов
вычесть произведение элементов 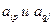 , расположенных в противоположных вершинах прямоугольника, деленное на разрешающий элемент
, расположенных в противоположных вершинах прямоугольника, деленное на разрешающий элемент 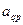
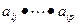
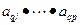
Аналогичным образом можно преобразовать систему (2) приняв за разрешающий элемент матрицы 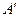 элемент
элемент 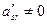 , причем s
, причем s 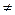 q,
q, 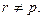 После этого преобразования все коэффициенты при
После этого преобразования все коэффициенты при 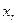 , кроме
, кроме 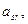 обратятся в нуль. Полученная система может быть снова преобразована и т.д. Если r = n (ранг системы равен числу неизвестных), то после ряда преобразований придем к системе уравнений вида
обратятся в нуль. Полученная система может быть снова преобразована и т.д. Если r = n (ранг системы равен числу неизвестных), то после ряда преобразований придем к системе уравнений вида
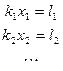
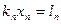
из которой находятся значения неизвестных.
Описанный метод решения, основанный на последовательном исключении неизвестных, называется методом Жордана-Гаусса.
Пример. Решить систему уравнений методом Жордана-Гаусса
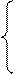
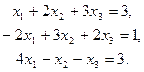
Запишем коэффициенты, свободные члены и суммы коэффициентов и свободных (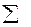 – контрольный столбец) членов в следующую таблицу
– контрольный столбец) членов в следующую таблицу
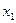 | 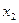 | 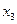 | 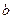 |  |
| -2 | ||||
| -1 | -1 |
Возьмем за разрешающий элемент коэффициент при 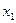 , в первом уравнение. Перепишем таблицу, где первая строка будет без изменения, а все элементы первого столбца будут равны нулю.
, в первом уравнение. Перепишем таблицу, где первая строка будет без изменения, а все элементы первого столбца будут равны нулю.
Применив правило прямоугольника, заполним остальные клетки.
 | 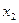 | 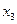 | 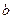 | 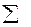 |
| -9 | -13 | -9 | -31 |
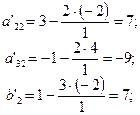
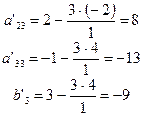
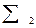 =4-
=4- 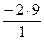 = 22
= 22 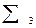 =5-
=5- 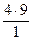 = -31.
= -31.
За разрешающий элемент возьмем коэффициент при 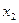 во втором уравнении. Перепишем таблицу, где вторая строка будет без изменения, а элементы второго столбца будут равны нулю (кроме разрешающего элемента).
во втором уравнении. Перепишем таблицу, где вторая строка будет без изменения, а элементы второго столбца будут равны нулю (кроме разрешающего элемента).
Остальные клетки заполним, применив правило прямоугольника.
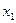 | 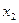 | 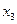 | 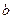 | 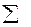 |
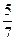 | 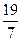 | |||
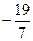 | - 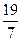 |
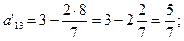
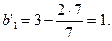
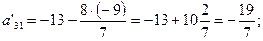
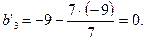
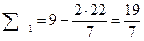 ;
;  =-31-
=-31- 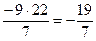
Первую и третью строку умножим на 7
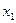 |  | 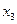 | 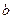 | 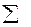 |
| -19 | -19 |
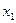 | 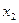 | 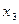 | 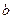 | 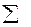 |
| -19 | -19 |
За разрешающий элемент возьмем коэффициент при 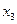 в третьем уравнении. Перепишем таблицу, где третья стока будет без изменения, элементы третьего столбца будут равны нулю, кроме разрешающего элемента.
в третьем уравнении. Перепишем таблицу, где третья стока будет без изменения, элементы третьего столбца будут равны нулю, кроме разрешающего элемента.
Остальные клетки заполним, применив правило прямоугольника.
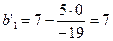
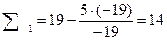
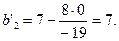
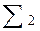 =22-
=22- 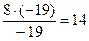
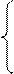 Получим
Получим 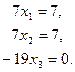 Отсюда
Отсюда 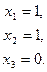 – един. решение.
– един. решение.
I:
S: Столбец неизвестных системы линейных уравнений это
-: 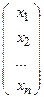
-: 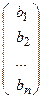
-: 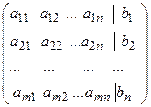
-: 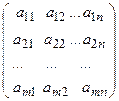
I:
S: Столбец свободных коэффициентов системы линейных уравнений это
-: 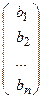
-: 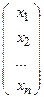
-: 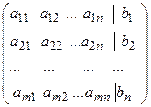
-: 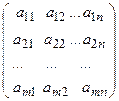
I:
S: Матрица вида 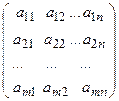 системы линейных уравнений, состоящая из коэффициентов называется
системы линейных уравнений, состоящая из коэффициентов называется
-: матрицей системы
-: расширенной матрицей
-: определителем
-: столбцом неизвестных
I:
S: Решение системы 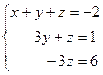 есть
есть
-: (-1; 1; -2)
-: (2; 1; 3)
-: (0; 5; 1)
-: (-2; 0; 0)
I:
S: Для определения элемента 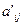 матрицы
матрицы 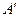 полезно иметь в виду
полезно иметь в виду
+: “правило прямоугольника”.
-: “правило треугольника”.
-: коэффициенты и свободные члены этой системы
-: свободные члены этой системы
I:
S: Методом Жордана-Гаусса коэффициенты и свободные члены системы определяются по формулам
+: 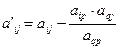 и
и 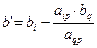
-: 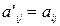 и
и 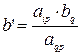
-: 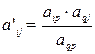 и
и 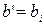
-: 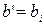 и
и 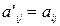
I:
S: Элемент 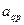 отличный от нулю называется
отличный от нулю называется
-: разрешающим элементом
-: свободным элементом
-: неизвестным элементом
-: нулевым элементом
 2015-01-21
2015-01-21 2348
2348
