2015-01-21
1885
Для исследования систем линейных уравнений и нахождения их решений можно использовать метод Гаусса.
Метод Гаусса состоит из двух этапов – прямой и обратный ход.
На первом этапе (прямой ход) расширенная матрица системы приводится к ступенчатому виду с помощью элементарных преобразований. Определяя ранг, полученной ступенчатой матрицы делаем вывод о совместности или несовместности, определенности или неопределенности системы линейных уравнений.
На втором этапе (обратный ход) полученной ступенчатой матрице составляют, соответствующую систему уравнений
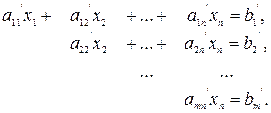
Исследовать системы линейных уравнений означает определить, совместна или нет, а для совместной системы – вычислить, определенна она или нет. При этом возможны три случая:
1) Если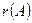 
< 
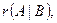то система несовместна.
2) Если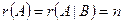 
(где n число неизвестных), то система совместна и определенна.
3) Если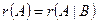 
< 
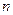, то система совместна и неопределенна.
где 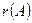- ранг матрицы системы,
где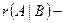 
ранг расширенной матрицы системы.
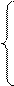Пример 1. Исследовать системы линейных уравнений. Для совместных систем найти общее и одно частное решение:
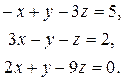
Решение.
Запишем расширенную матрицу системы и приведем к ступенчатому виду с помощью элементарных преобразований.
~ 
~ 
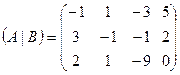
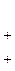
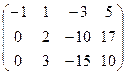
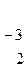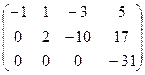
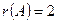
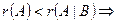система несовместна (т.е. нет решений)
 |
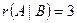
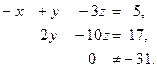
Ответ: несовместна (нет решений).
Пример 2.
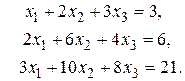
Решение.
Запишем расширенную матрицу системы и приведем к ступенчатому виду с помощью элементарных преобразований.
 | |
~ 
~ 
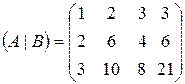
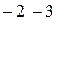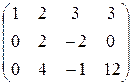
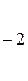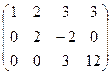
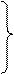
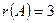
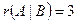
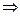система совместна и определенна (т.е. имеет
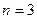- (число неизвестных) един. решение)
.
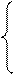
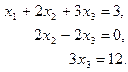
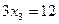
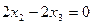
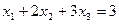
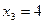
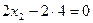
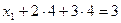
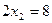
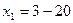
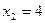
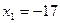Ответ: (-17;4;4).
Пример 3. Решить систему методом Гаусса
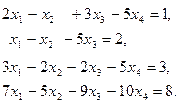
Решение.
Запишем расширенную матрицу системы и приведем ее к ступенчатому виду с помощью элементарных преобразований.
~ 
~
~ 
< 
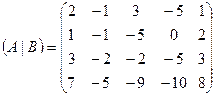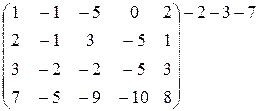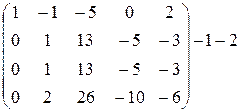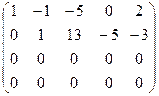
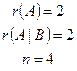
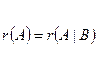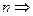система имеет бесконечное множество решений.
Запишем систему соответствующую полученной матрице:
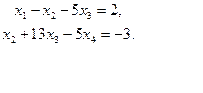
Обозначим свободные переменные: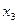 
через 
, 
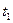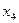через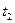 
.
Общее решение системы
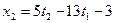
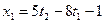
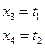
Если положить, например,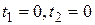 
, то найдем одно частное решение
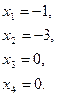
I:
S: Матрица системы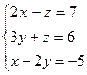 
имеет вид
-: 
-: 
-: 
-: 
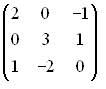
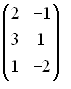
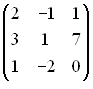
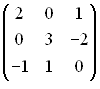
I:
S: Расширенная матрица системы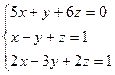 
имеет вид
-: 
-: 
-: 
-: 
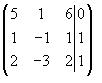
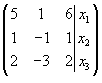
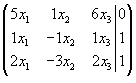
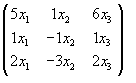
I:
S: Решение системы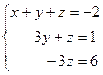 
есть
-: (-1; 1; -2)
-: (2; 1; 3)
-: (0; 5; 1)
-: (-2; 0; 0)
I:
S: Ранг матрицы системы равен рангу расширенной матрицы и меньше числа неизвестных, то система имеет
-: бесконечное множество решений
-: единственное решение
-: не имеет решений
-: только нулевое решение
I:
S: Ранг матрицы системы равен рангу расширенной матрицы и числу неизвестных, то система имеет
-: единственное решение
-: бесконечное множество решений
-: не имеет решений
-: только нулевое решение
I:
S: Ранг матрицы системы меньше ранга расширенной матрицы, то система
-: не имеет решений
-: единственное решение
-: бесконечное множество решений
-: только нулевое решение
I:
S: Матрица вида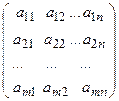 
системы линейных уравнений, состоящая из коэффициентов называется
-: матрицей системы
-: расширенной матрицей
-: определителем
-: столбцом неизвестных
