Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ox, Oy, Oz единичные векторы 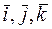
 z
z













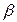
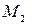
O 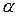 y
y

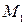 N
N
x
Выберем произвольный вектор 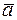 и совместим его начало с началом координат. Найдём проекции вектора на координатные оси. Проведём через конец вектора
и совместим его начало с началом координат. Найдём проекции вектора на координатные оси. Проведём через конец вектора 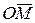 плоскости параллельные координатным плоскостям. Точки пересечения обозначим через
плоскости параллельные координатным плоскостям. Точки пересечения обозначим через 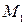 ,
, 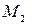 ,
, 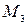 . Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 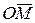 .Тогда
.Тогда 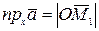 ,
, 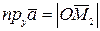 ,
, 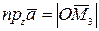 .По определению суммы нескольких векторов находим
.По определению суммы нескольких векторов находим 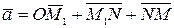 .
.
А так как 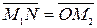
 ,
, 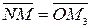 , то
, то
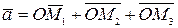 .
.
Но
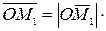
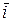 ,
, 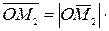
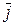 ,
, 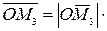
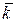
Обозначим проекции вектора 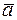 =
= 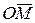 на оси Ox, Oy, Oz соответственно через
на оси Ox, Oy, Oz соответственно через
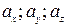 т.е.
т.е. 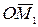
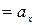 ,
, 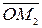
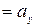 ,
, 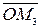
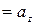 . Тогда получаем
. Тогда получаем
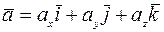 .
.
Эта формула называется разложением вектора по ортам координатных осей.
Направление вектора 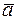 определяется с помощью направляющих косинусов:
определяется с помощью направляющих косинусов: 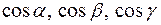
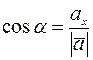 ,
, 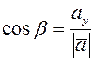 ,
, 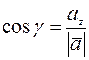 , где
, где 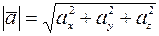 - длина вектора.
- длина вектора.
Направляющие косинусы связаны соотношением 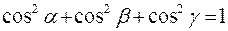 .
.
 2015-01-21
2015-01-21 3000
3000
