2015-01-21
545
Вектором называется направленный отрезок.
Вектор с началом в точке А и концом в точке В обозначается символом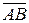 
или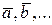 
. Длина отрезка АВ называется длиной, или модулям вектора .
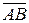Вектор длина, которого равна единице, называется единичным и обозначается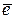 
.
Вектор длина, которого равна нулю, называется нулевым и обозначается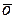 
.
Единичный вектор, направление которого совпадает с направлением вектора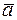 
, называется ортом и обозначается 
.
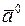Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Два коллинеарных вектора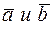 
называются равными (
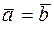), если они сонаправлены и имеют равные длины.
Углом между векторами 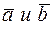называется угол при вершине этого треугольника, соответствующий началу векторов. Сумой двух векторов 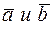называется вектор 
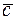, соединяющий начало вектора 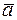с концом вектора 
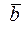, отложенного от конца вектора 
.
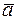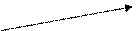
Для геом. представления суммы векторов используется правила «треугольников» и «параллелограмма».
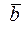
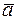
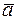
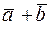
Рис.1
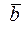
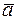
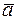
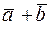
О 
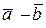
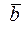
Произведением вектора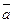 
на скаляр (число) 
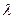называется вектор 
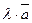( или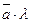 
), который имеет длину 
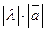, коллинеарен вектору 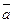имеет направление вектора ,
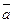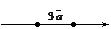
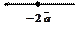если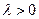 
и противоположное направление, если 
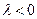. Например, если дан вектор,
то векторы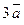 
и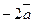 
будут иметь вид и.
Из определения произведения вектора на число следуют свойства этого произведения:
1) если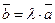 
, то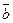 
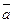|| . Наоборот, если || , (
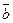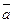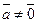), то при некотором 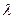верно равенство ;
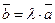2) всегда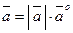 
, т.е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1. 
,
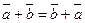2. 
,
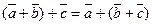3. 
,
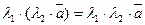4. 
,
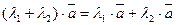5. 
.
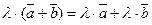Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители
