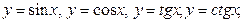2015-01-21
985
Определение. Функцией (числовой функцией) называется отображение числового множества D в числовое множество Е.
Функцию записывают так: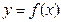 
. Множество D называется областью определения функции, а его элемент 
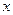- аргументом. Множество Е называется областью значений функции, а его элемент 
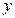- функцией (значением функции, зависимой переменной).
Для того, чтобы функция была определена, надо знать: а) область определения D; б) закон, по которому каждому числу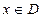 
ставится в соответствие число 
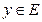. Как следует из определения функции, каждому 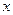соответствует только одно 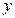, но это вовсе не исключает того, что разным значениям 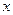могут соответствовать одинаковые значения 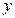. Закон, по которому задается функция, можно задать разными способами: формулой (аналитический способ), графиком (графический способ), таблицей (табличный способ), словесной формулировкой.
Графиком функции 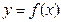называют множество точек на плоскости, у которых абсциссы являются допустимыми значениями аргумента 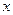, а ординаты – соответствующими значениями функции .
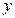График функции представляет собой некоторую кривую на плоскости.
К основным элементарным функциям относятся следующие:
1. Степенная функция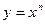 
(
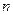- постоянное действительное число). При 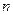=0 степенная функция есть постоянная величина 
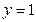; при 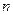=1 получается функция 
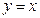(прямая пропорциональная зависимость); если 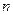=2, то степенная функция 
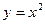является квадратичной; если 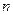=-1, то получается обратно пропорциональная зависимость 
.
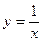2. Показательная функция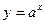 
(
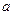- положительное число, 
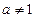). Особую роль в математике играет показательная функция с основанием 
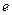, то есть функция 
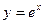. Число 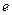- иррациональное число, 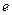=2,718281828459… Функцию 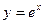называют экспоненциальной функцией.
3. Логарифмическая функция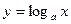 
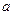( - положительное число, 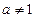). На практике часто используют логарифмы по основанию 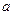=10 – десятичные логарифмы. Для десятичного логарифма принята запись 
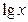. Основание 
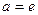также играет особую роль, логарифм по основанию 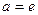обозначают следующим образом: 
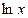и называют натуральным логарифмом числа .
.
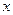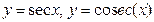5. Обратные тригонометрические функции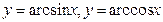 
,
.
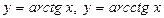Функции, которые получаются из основных элементарных функций с помощью конечного числа арифметических операций (сложения, вычитания, умножения и деления) и операций «взятие функции от функции», называются элементарными функциями. Операцию «взятие функции от функции» также называют композицией функций. Функция, в которой вместо переменной записана другая элементарная функция называется сложной функцией и также относится к множеству элементарных функций.
